如图,在四棱锥P-ABCD中,底面ABCD是矩形,M、N分别为PA、BC的中点, PD⊥平面ABCD,且PD=AD=
PD⊥平面ABCD,且PD=AD= ,CD=1
,CD=1
(1)证明:MN∥平面PCD;
(2)证明:MC⊥BD;
(3)求二面角A—PB—D的余弦值。
某班共有学生40人,将一次数学考试成绩(单位:分)绘制成频率分布直方图,如图所示.
(1)请根据图中所给数据,求出a的值;
(2)为了了解学生本次考试的失分情况,从成绩在[50,70)内的学生中随机选取3人的成绩进行分析,用X表示所选学生成绩在[60,70)内的人数,求X的分布列和数学期望.
数列
 是递增的等比数列,且
是递增的等比数列,且 .
.
(Ⅰ)若 ,求证:数列
,求证:数列 是等差数列;
是等差数列;
(Ⅱ)若
 ,求
,求 的最大值.
的最大值.
已知函数 的图象经过点
的图象经过点 .
.
(1)求函数 的最小正周期与单调递增区间.
的最小正周期与单调递增区间.
(2)若 ,且
,且 ,求
,求 的值.
的值.
(本小题满分13分)已知函数 .
.
(Ⅰ)当 时,求函数
时,求函数 的极值;
的极值;
(Ⅱ)
 时,讨论
时,讨论 的单调性;
的单调性;
(Ⅲ)若对任意的 恒有
恒有 成立,求实数
成立,求实数 的取值范围.
的取值范围.
(本小题满分13分)已知函数 .
.
(Ⅰ)求函数 的定义域;
的定义域;
(Ⅱ)若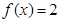 ,求
,求 的取值集合及
的取值集合及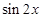 的值.
的值.