如图四棱锥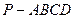 中,
中, 底面
底面 ,
, 正方形的边长为2
正方形的边长为2
(1)求点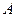 到平面
到平面 的距离;
的距离;
(2)求直线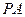 与平面
与平面 所成角的大小;
所成角的大小;
(3)求以 与
与 为半平面的二面角的正切值。
为半平面的二面角的正切值。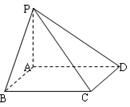
如图正方体ABCD-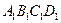 中,E、F、G分别是
中,E、F、G分别是 、AB、BC的中点.
、AB、BC的中点.
(1)证明: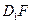 ⊥EG;
⊥EG;
(2)证明: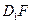 ⊥平面AEG;
⊥平面AEG;
(3)求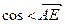 ,
,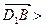 .
.
如图,四棱锥P—ABCD的底面是AB=2,BC= 的矩形,侧面PAB是等边三角形,且侧面PAB⊥底面ABCD
的矩形,侧面PAB是等边三角形,且侧面PAB⊥底面ABCD
(I)证明:侧面PAB⊥侧面PBC;
(II)求侧棱PC与底面ABCD所成的角;
(III)求直线AB与平面PCD的距离.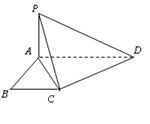
如图,棱锥P—ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD= .
.
(Ⅰ)求证:BD⊥平面PAC;
(Ⅱ)求二面角P—CD—B的大小;
(Ⅲ)求点C到平面PBD的距离. 
在直角梯形P1DCB中,P1D//CB,CD//P1D且P1D = 6,BC = 3,DC = ,A是P1D的中点,沿AB把平面P1AB折起到平面PAB的位置,使二面角P-CD-B成45°角,设E、F分别是线段AB、PD的中点.
,A是P1D的中点,沿AB把平面P1AB折起到平面PAB的位置,使二面角P-CD-B成45°角,设E、F分别是线段AB、PD的中点.
(1)求证:AF//平面PEC;
(2)求平面PEC和平面PAD所成的二面角的大小;
(3)求点D到平面PEC的距离.
