如图四棱锥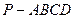 中,
中, 底面
底面 ,
, 正方形的边长为2
正方形的边长为2
(1)求点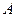 到平面
到平面 的距离;
的距离;
(2)求直线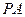 与平面
与平面 所成角的大小;
所成角的大小;
(3)求以 与
与 为半平面的二面角的正切值。
为半平面的二面角的正切值。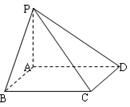
请您设计一个帐篷。它下部的形状是高为1m的正六棱柱,上部的形状是侧棱长为3m的正六棱锥(如右图所示)。试问当帐篷的顶点O到底面中心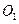 的距离为多少时,帐篷的体积最大?
的距离为多少时,帐篷的体积最大?
路灯距地平面为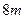 ,一个身高为
,一个身高为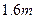 的人以
的人以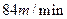 的速率在地面上行走,从路灯在地平面上射影点C,沿某直线离开路灯,求人影长度的变化速率v.
的速率在地面上行走,从路灯在地平面上射影点C,沿某直线离开路灯,求人影长度的变化速率v.
(本小题满分12分) 已知向量
已知向量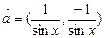 ,
,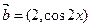 .(1)若
.(1)若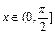 ,试判断
,试判断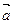 与
与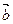 能否平行?(2)若
能否平行?(2)若 ,求函数
,求函数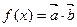 的最小值.
的最小值.
(本小题满分14分)
已知圆 方程为:
方程为: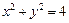 .
. (1)直线
(1)直线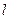 过点
过点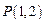 ,且与圆
,且与圆 交于
交于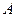 、
、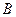 两点,若
两点,若 ,求直线
,求直线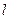 的方程;
的方程; (2)过圆
(2)过圆 上一动点
上一动点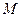 作平行于
作平行于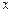 轴的直线
轴的直线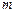 ,设
,设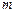 与
与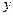 轴的交点为
轴的交点为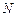 ,若向量
,若向量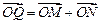 ,求动点
,求动点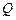 的轨迹方程,并说明此轨迹是什么曲线.
的轨迹方程,并说明此轨迹是什么曲线.
(本小题满分14分) 已知椭圆
已知椭圆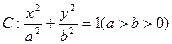 的离心率为
的离心率为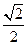 ,且曲线过点
,且曲线过点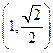
 (1)求椭圆C的方程;
(1)求椭圆C的方程; (2)已知直线
(2)已知直线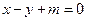 与椭圆C交于不同的两点A,B,且线段AB的中点不在圆
与椭圆C交于不同的两点A,B,且线段AB的中点不在圆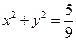 内,求
内,求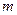 的取值范围.
的取值范围.
