某校的高二(一)班男同学有45名,女同学有 名,老师按照分层抽样的方法组建了一个
名,老师按照分层抽样的方法组建了一个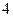 人的课外兴趣小组.
人的课外兴趣小组.
(1)求某同学被抽到的概率及课外兴趣小组中男、女同学的人数;
(2)经过一个月的学习、讨论,这个兴趣小组决定选出两名同学做某项实验,方法是先从小组里选出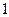 名同学做实验,该同学做完后,再从小组内剩下的同学中选一名同学做实验,求选出的两名同学中恰有一名女同学的概率;
名同学做实验,该同学做完后,再从小组内剩下的同学中选一名同学做实验,求选出的两名同学中恰有一名女同学的概率;
(3)试验结束后,第一次做试验的同学得到的试验数据为 ,第二次做试验的同学得到的试验数据为
,第二次做试验的同学得到的试验数据为 ,请问哪位同学的实验更稳定?并说明理由.
,请问哪位同学的实验更稳定?并说明理由.
(本小题满分13分)某租赁公司拥有汽车100辆.当每辆车的月租金为3000元时,可全部租出。当每辆车的月租金每增加50元时,未租出的车将会增加一辆。租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元。(1)当每辆车的月租金定为3600元时,能租出多少辆车?(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
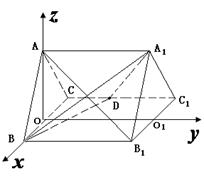
如图,正三棱柱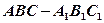 的所有棱长都为2,
的所有棱长都为2, 为
为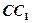 中点,试用空间向量知识解下列问题:
中点,试用空间向量知识解下列问题:
(1)求证 面
面 ;
;
(2)求二面角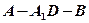 的大小。
的大小。
(选修4-3坐标系与参数方程)
求直线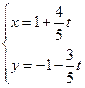 (
( )被曲线
)被曲线 所截的弦长.
所截的弦长.
(选修4-1 几何证明选讲)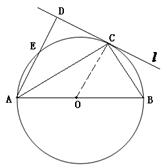
如图,圆O的直径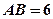 ,
,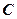 为圆周上一点,
为圆周上一点, ,过
,过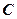 作圆的切线
作圆的切线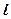 ,过A作
,过A作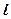 的垂线AD,AD分段别与直线
的垂线AD,AD分段别与直线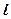 、圆交于点D、E。求
、圆交于点D、E。求 的度数与线段AE的长。
的度数与线段AE的长。
(本题16分) 设函数 ,且
,且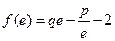 ,其中
,其中 是自然对数的底数.(1)求
是自然对数的底数.(1)求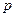 与
与 的关系;(2)若
的关系;(2)若 在其定义域内为单调函数,求
在其定义域内为单调函数,求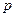 的取值范围;
的取值范围;
(3)设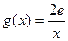 ,若在
,若在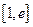 上至少存在一点
上至少存在一点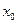 ,使得
,使得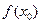 >
> 成立,求实数
成立,求实数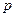 的取值范围.
的取值范围.