已知一个三角形的三边边长分别为 ,设计一个算法,求出它的面积。
,设计一个算法,求出它的面积。
已知椭圆 :
: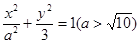 的右焦点
的右焦点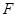 在圆
在圆 上,直线
上,直线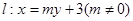 交椭圆于
交椭圆于 、
、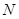 两点.
两点.
(1)求椭圆 的方程;
的方程;
(2)若 (
( 为坐标原点),求
为坐标原点),求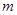 的值;
的值;
PM2.5是指悬浮在空气中的空气动力学当量直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.根据现行国家标准GB3095-2012, PM2.5日均值在35微克/立方米以下空气质量为一级;在35~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.从某自然保护区2012年全年每天的PM2.5监测值数据中随机地抽取12天的数据作为样本,监测值频数如茎叶图所示(十位为茎,个位为叶):
(I)求空气质量为超标的数据的平均数与方差;
(II)从空气质量为二级的数据中任取2个,求这2个数据的和小于100的概率;
(III)以这12天的PM2.5日均值来估计2012年的空气质量情况,估计2012年(366天)大约有多少天的空气质量达到一级或二级.
如图,已知长方形ABCD中,AB=2,A1,B1分别是AD,BC边上的点,且AA1=BB1="1," E,F分别为B1D与AB的中点. 把长方形ABCD沿直线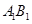 折成直角二面角,且
折成直角二面角,且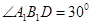 .
.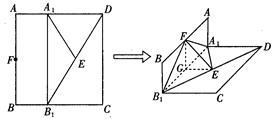
(1)求证: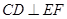
(2)求三棱锥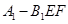 的体积.
的体积.
在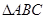 内,
内,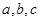 分别为角
分别为角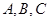 所对的边,
所对的边,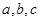 成等差数列,且
成等差数列,且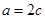 .
.
(Ⅰ)求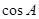 的值;(Ⅱ)若
的值;(Ⅱ)若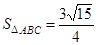 ,求
,求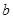 的值。
的值。
已知数列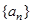 的前
的前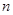 项和为
项和为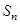 ,且
,且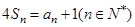 .
.
(Ⅰ)求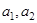 ;(Ⅱ)设
;(Ⅱ)设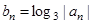 ,求数列
,求数列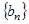 的通项公式。
的通项公式。