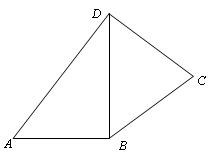
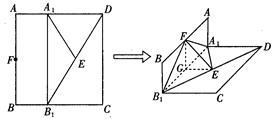
如图,已知长方形ABCD中,AB=2,A1,B1分别是AD,BC边上的点,且AA1=BB1="1," E,F分别为B1D与AB的中点. 把长方形ABCD沿直线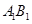 折成直角二面角,且
折成直角二面角,且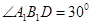 .
.
(1)求证: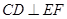
(2)求三棱锥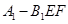 的体积.
的体积.
(本小题满分10分)
某工厂生产甲、乙两种产品,每种产品都要经过第一和第二道工序加工 而成,两道工序的加工结果相互独立,每道工序的加工结果都有A、B两个等级,每种产品只有两道工序的加工结果都为A等级时,才为一等品,其余均为二等品。
而成,两道工序的加工结果相互独立,每道工序的加工结果都有A、B两个等级,每种产品只有两道工序的加工结果都为A等级时,才为一等品,其余均为二等品。
(I)已知甲、乙两种产品每道工序的加工结果为A等级的概率如表一所示,分别求工厂生产甲、乙产品为一等品的概率P甲和P乙;
(II)已知一件产品的利润如表二所示,用 、
、 分别表示一件甲、乙产品的利润,在(I)的条件下,求
分别表示一件甲、乙产品的利润,在(I)的条件下,求 、
、 的分布列及其数学期望.
的分布列及其数学期望.
(本小题满分12分)
已知
(I)求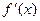 ;
;
(II)若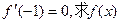 在[—2,4]上的最大值.
在[—2,4]上的最大值.
(本小题满分 12分
12分 )
)
在对人们休闲方式的一次调查中,共调查120人,其中女性70人、男性50人,女性中有40人主要的休闲方式是看电视,另外30人主要的休闲方式是运动;男性中有20人主要的休闲方式是看电视,另外30人主要的休闲方式是运动。 (I)根据以上数据建立一个2×2的列联表:
(I)根据以上数据建立一个2×2的列联表:
| 休闲方式 性别 |
看电视 |
运动 |
总计 |
| 女性 |
|||
| 男性 |
|||
| 总计 |
(II)休闲方式与性别是否有关?
(本小题满分10分) 已知
已知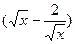 二项展开式中,第4项的二项式系数与第3项的二项式系数的比为8:3.
二项展开式中,第4项的二项式系数与第3项的二项式系数的比为8:3.
(I)求n的值; (II)求展开式中
(II)求展开式中 项的系数.
项的系数.
(本小题满分12分)
如图,四边形ABCD是平面图形,BC=CD=1,AB=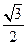 BD,
BD, 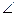 ABD=
ABD= ,设
,设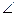 BCD=
BCD= ,四边形ABCD的面积为S,求函数S=
,四边形ABCD的面积为S,求函数S= 的最大值.
的最大值.