有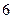 个球,其中
个球,其中 个黑球,红、白、蓝球各
个黑球,红、白、蓝球各 个,现从中取出
个,现从中取出 个球排成一列,共有多少种不同的排法?
个球排成一列,共有多少种不同的排法?
(本小题满分13分)
设数列 的前
的前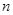 项和为
项和为 ,若对任意的正整数
,若对任意的正整数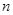 ,总存在正整数
,总存在正整数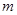 ,使得
,使得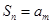 ,则称
,则称 是“
是“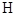 数列”。
数列”。
(1)若数列 的前
的前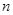 项和为
项和为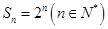 ,证明:
,证明: 是“
是“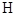 数列”;
数列”;
(2)设 是等差数列,其首项
是等差数列,其首项 ,公差
,公差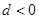 ,若
,若 是“
是“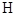 数列”,求
数列”,求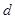 的值;
的值;
(3)证明:对任意的等差数列 ,总存在两个“
,总存在两个“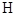 数列”
数列” ,使得
,使得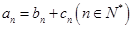 成立。
成立。
(本小题满分12分)已知函数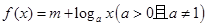 的图像过点
的图像过点 ,点
,点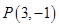 关于直线
关于直线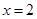 的对称点
的对称点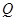 在
在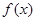 的图像上。
的图像上。
(1)求函数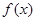 的解析式;
的解析式;
(2)令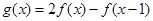 ,求
,求 的最小值及取得最小值时
的最小值及取得最小值时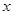 的值。
的值。
(本小题满分12分)函数
(1)讨论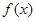 的单调性;
的单调性;
(2)若函数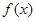 在区间
在区间 上是增函数,求
上是增函数,求 的取值范围。
的取值范围。
(本小题满分12分)如图,直三棱柱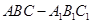 中,
中,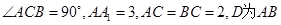 的中点,
的中点, 上一点,且
上一点,且
(1)当 时,求证:
时,求证: ;
;
(2)若直线 与平面
与平面 所成的角为
所成的角为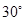 ,求
,求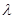 的值。
的值。
(本小题满分12分)已知函数 的图像关于直线
的图像关于直线 对称,且图像上相邻两个最高点的距离为
对称,且图像上相邻两个最高点的距离为 。
。
(1)求 和
和 的值;
的值;
(2)若 ,求
,求 的值。
的值。