(本小题满分13分)
设数列 的前
的前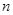 项和为
项和为 ,若对任意的正整数
,若对任意的正整数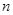 ,总存在正整数
,总存在正整数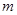 ,使得
,使得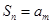 ,则称
,则称 是“
是“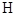 数列”。
数列”。
(1)若数列 的前
的前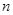 项和为
项和为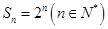 ,证明:
,证明: 是“
是“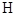 数列”;
数列”;
(2)设 是等差数列,其首项
是等差数列,其首项 ,公差
,公差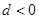 ,若
,若 是“
是“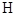 数列”,求
数列”,求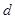 的值;
的值;
(3)证明:对任意的等差数列 ,总存在两个“
,总存在两个“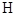 数列”
数列” ,使得
,使得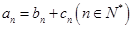 成立。
成立。
如图,在正方体 中,
中, 分别为
分别为 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)求证:平面 平面
平面 .
.
在平面直角坐标系 中,设锐角
中,设锐角 的始边与
的始边与 轴的非负半轴重合,终边与单位圆交于点
轴的非负半轴重合,终边与单位圆交于点 ,将射线
,将射线 绕坐标原点
绕坐标原点 按逆时针方向旋转
按逆时针方向旋转 后与单位圆交于点
后与单位圆交于点 . 记
. 记 .
.
(1)求函数 的值域;
的值域;
(2)设 的角
的角 所对的边分别为
所对的边分别为 ,若
,若 ,且
,且 ,
, ,求
,求 .
.
(本小题满分14分)已知函数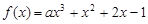 (
(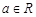 ).
).
(1)求曲线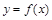 在点
在点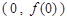 处的切线方程;
处的切线方程;
(2)是否存在常数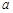 ,使得
,使得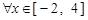 ,
,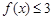 恒成立?若存在,求常数
恒成立?若存在,求常数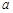 的值或取值范围;若不存在,请说明理由.
的值或取值范围;若不存在,请说明理由.
(本小题满分14分)在平面直角坐标系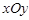 中,椭圆
中,椭圆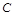 的焦点为
的焦点为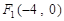 、
、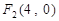 ,且经过点
,且经过点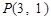 .
.
(1)求椭圆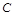 的标准方程;
的标准方程;
(2)若点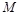 在椭圆
在椭圆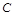 上,且
上,且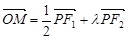 ,求
,求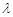 的值.
的值.
(本小题满分12分)某农户建造一间背面靠墙的小房,已知墙面与地面垂直,房屋所占地面是面积为12 m2的矩形,房屋正面每平方米的造价为1200元,房屋侧面每平方米的造价为800元,屋顶的造价为5200元.如果墙高为3 m,且不计房屋背面和地面的费用,问怎样设计房屋能使总造价最低?最低总造价是多少?