已知定义在R上的函数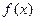
和数列
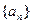满足下列条件：
，
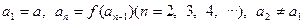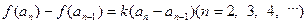，其中a为常数，k为非零常数.
（Ⅰ）令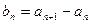
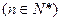，证明数列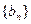
是等比数列；
（Ⅱ）求数列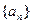的通项公式；
（III）当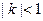
时，求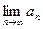
.
(本题满分12分)
已知直线
与圆
交于
两点，
为原点，求
（1）
的数量积；（2）
为何值时，两向量夹角为
。
(本题满分12分)
阅读以上流程图，若记y=f（x）
（1）写出y=f(x)的解析式，并求函数的值域，
（2）若x0满足f(x0)＜0 且f(f(x0))=1,求x0.
(本题满分10分)
对甲、乙两名自行车赛手在相同条件下进行了6次测试,测得他们的最大速度(m/s)的数据如下表:
| 甲 |
27 |
38 |
30 |
37 |
35 |
31 |
| 乙 |
33 |
29 |
38 |
34 |
28 |
36 |
（1）画出茎叶图；
（2）分别求出甲、乙两名自行车赛手最大速度数据的平均数、标准差（精确到0.01）,并判断选谁参加比赛更合适.
（本小题满分12分）
已知数列
满足：
，且对一切
，有
，其中
为数列的前
项和．（Ⅰ）求数列的通项公式；
（Ⅱ）证明：
．
（本小题满分12分）
已知
，函数
在
处取得极值，曲线
过原点
和点
．若曲线在点
处的切线
与直线
的夹角为
，且直线的倾斜角
（Ⅰ）求
的解析式；（Ⅱ）若函数在区间
上是增函数，求实数
的取值范围；（Ⅲ）若
、
，求证：