某化工厂引进一条先进生产线生产某种化工产品,其生产的总成本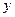 (万元)与年产量
(万元)与年产量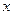 (吨)之间的函数关系式可以近似地表示为
(吨)之间的函数关系式可以近似地表示为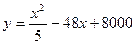 ,已知此生产线年产量最大为210吨。
,已知此生产线年产量最大为210吨。
(1)求年产量为多少吨时,生产每吨产品的平均成本最低,并求最低成本;
(2)若每吨产品平均出厂价为40万元,那么当年产量为多少吨时,可以获得最大利润?最大利润是多少?
某停车场临时停车按时段收费,收费标准为:每辆汽车一次停车不超过1小时收费6元,超过1小时的部分每小时收费8元(不足1小时的部分按1小时计算).现有甲、乙二人在该停车场临时停车,两人停车都不超过4小时.
(1)若甲停车1小时以上且不超过2小时的概率为 ,停车付费多于14元的概率为
,停车付费多于14元的概率为 ,求甲临时停车付费恰为6元的概率;
,求甲临时停车付费恰为6元的概率;
(2)若每人停车的时间在每个时段的可能性相同,求甲、乙二人停车付费之和为36元的概率.
一个袋中有4个大小相同的小球,其中红球1个,白球2个,黑球1个,现从袋中有放回地取球,每次随机取1个.
(1)求连续取两次都是白球的概率;
(2)若取1个红球记2分,取1个白球记1分,取1个黑球记0分,求连续取两次的分数之和为2的概率.
如图所示的茎叶图记录了甲组3名同学寒假假期中去图书馆A学习的次数和乙组4名同学寒假假期中去图书馆B学习的次数.乙组记录中有一个数据模糊,无法确认,在图中以x表示.
(1)如果x=7,求乙组同学去图书馆学习次数的平均数和方差;
(2)如果x=9,从学习次数大于8的学生中选2名同学,求选出的2名同学恰好分别在两个图书馆学习且学习的次数和大于20的概率.
现有6道题,其中4道甲类题,2道乙类题,张同学从中任取2道题解答.试求:
(1)所取的2道题都是甲类题的概率;
(2)所取的2道题不是同一类题的概率.
函数 .
.
(1)若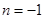 ,函数
,函数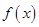 在区间
在区间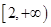 上是单调递增函数,求实数
上是单调递增函数,求实数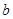 的取值范围;
的取值范围;
(2)设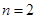 ,若对任意
,若对任意 恒成立,求
恒成立,求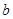 的取值范围.
的取值范围.