【2015高考陕西,文23】选修4-4:坐标系与参数方程
在直角坐标版权法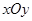 吕,直线
吕,直线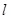 的参数方程为
的参数方程为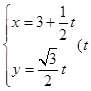 为参数),以原点为极点,
为参数),以原点为极点,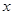 轴的正半轴为极轴建立极坐标系,
轴的正半轴为极轴建立极坐标系,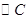 的极坐标方程为
的极坐标方程为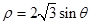 .
.
(Ⅰ)写出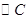 的直角坐标方程;
的直角坐标方程;
(Ⅱ)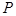 为直线
为直线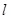 上一动点,当
上一动点,当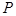 到圆心
到圆心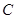 的距离最小时,求点
的距离最小时,求点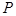 的坐标.
的坐标.
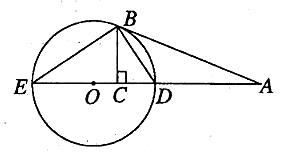
【2015高考陕西,文22】选修4-1:几何证明选讲
如图,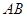 切
切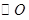 于点
于点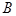 ,直线
,直线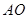 交
交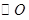 于
于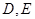 两点,
两点,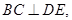 垂足为
垂足为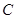 .
.
(Ⅰ)证明: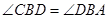
(Ⅱ)若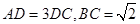 ,求
,求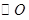 的直径.
的直径.
【2015高考重庆,文17】随着我国经济的发展,居民的储蓄存款逐年增长.设某地区城乡居民人民币储蓄存款(年底余额)如下表:
| 年份 |
2010 |
2011 |
2012 |
2013 |
2014 |
时间代号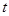 |
1 |
2 |
3 |
4 |
5 |
储蓄存款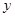 (千亿元) (千亿元) |
5 |
6 |
7 |
8 |
10 |
(Ⅰ)求y关于t的回归方程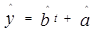
(Ⅱ)用所求回归方程预测该地区2015年(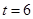 )的人民币储蓄存款.
)的人民币储蓄存款.
附:回归方程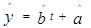 中
中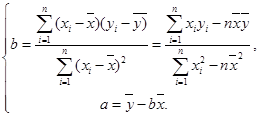
【2015高考新课标1,文19】(本小题满分12分)某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响,对近8年的宣传费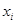 和年销售量
和年销售量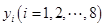 数据作了初步处理,得到下面的散点图及一些统计量的值.
数据作了初步处理,得到下面的散点图及一些统计量的值.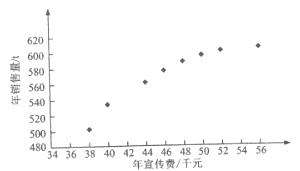
 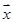 |
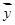 |
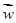 |
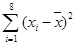 |
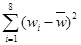 |
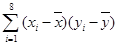 |
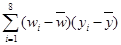 |
| 46.6 |
56.3 |
6.8 |
289.8 |
1.6 |
1469 |
108.8 |
表中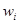 =
=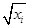 ,
,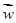 =
=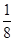
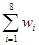
(Ⅰ)根据散点图判断,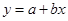 与
与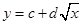 ,哪一个适宜作为年销售量y关于年宣传费x的回归方程类型(给出判断即可,不必说明理由);
,哪一个适宜作为年销售量y关于年宣传费x的回归方程类型(给出判断即可,不必说明理由);
(Ⅱ)根据(Ⅰ)的判断结果及表中数据,建立y关于x的回归方程;
(Ⅲ)已知这种产品的年利润z与x,y的关系为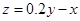 ,根据(Ⅱ)的结果回答下列问题:
,根据(Ⅱ)的结果回答下列问题:
(ⅰ)当年宣传费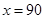 时,年销售量及年利润的预报值时多少?
时,年销售量及年利润的预报值时多少?
(ⅱ)当年宣传费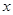 为何值时,年利润的预报值最大?
为何值时,年利润的预报值最大?
附:对于一组数据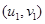 ,
,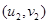 ,……,
,……,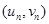 ,其回归线
,其回归线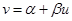 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: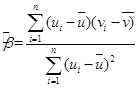 ,
,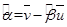
【2015高考天津,文15】(本小题满分13分)设甲、乙、丙三个乒乓球协会的运动员人数分别为27,9,18,先采用分层抽样的方法从这三个协会中抽取6名运动员参加比赛.
(Ⅰ)求应从这三个协会中分别抽取的运动员人数;
(Ⅱ)将抽取的6名运动员进行编号,编号分别为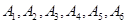 ,从这6名运动员中随机抽取2名参加双打比赛.
,从这6名运动员中随机抽取2名参加双打比赛.
(ⅰ)用所给编号列出所有可能的结果;
(ⅱ)设A为事件“编号为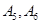 的两名运动员至少有一人被抽到”,求事件A发生的概率.
的两名运动员至少有一人被抽到”,求事件A发生的概率.