(本小题满分12分)(注意:在试题卷上作答无效)
已知双曲线 的右顶点为A,右焦点为F,右准线与
的右顶点为A,右焦点为F,右准线与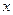 轴交于点B,且与一条渐近线交于点C,点O为坐标原点,又
轴交于点B,且与一条渐近线交于点C,点O为坐标原点,又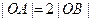 ,
,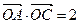 过点F的直线与双曲线右支交于点M、N,点P为点M关于
过点F的直线与双曲线右支交于点M、N,点P为点M关于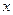 轴的对称点。
轴的对称点。
(Ⅰ)求双曲线的方程;
(Ⅱ)证明:B、P、N三点共线;
某企业投入81万元经销某产品,经销时间共60个月,市场调研表明,该企业在经销这个产品期间第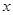 个月的利润
个月的利润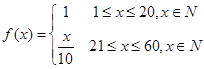 (单位:万元),
(单位:万元),
为了获得更多的利润,企业将每月获得的利润投入到次月的经营中,即第x个月的当月利润率 例如:
例如:
(1)求 ;
;
(2)求第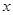 个月的当月利润率
个月的当月利润率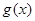 ;
;
(3)该企业经销此产品期间,哪个月的当月利润率最大,并求该月的当月利润率。
已知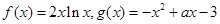 。
。
(1)求函数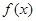 的最小值;
的最小值;
(2)若存在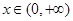 ,使
,使 成立,求实数
成立,求实数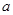 的取值范围。
的取值范围。
已知函数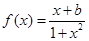 为奇函数。
为奇函数。
(1)判断函数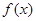 在区间(1,
在区间(1,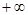 )上的单调性;
)上的单调性;
(2)解关于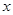 的不等式:
的不等式: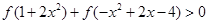 。
。
已知函数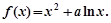
(1)当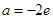 时,求函数
时,求函数 的单调区间;
的单调区间;
(2)若函数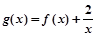 在[1,3]上是减函数,求实数
在[1,3]上是减函数,求实数 的取值范围。
的取值范围。
定义在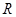 上的函数
上的函数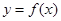 ,
, ,当
,当 时,
时, ,且对任意的
,且对任意的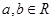 ,有
,有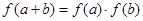 ,
,
(1)求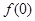 的值;
的值;
(2)求证:对任意的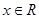 ,恒有
,恒有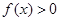 ;
;
(3)判断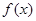 的单调性,并证明你的结论。
的单调性,并证明你的结论。