(本小题满分14分)已知函数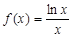 ,
, .
.
(Ⅰ)求函数 的单调区间;(Ⅱ)若函数
的单调区间;(Ⅱ)若函数 在[
在[ 上有零点,求
上有零点,求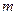 的最大值;(Ⅲ)证明:
的最大值;(Ⅲ)证明: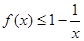 在其定义域内恒成立,并比较
在其定义域内恒成立,并比较 与
与 (
(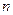
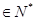 且
且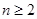 )的大小.
)的大小.
设计算法框图,要求输入自变量 的值,输出函数
的值,输出函数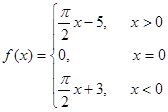 的值。
的值。
两台机床同时生产直径为10的零件,为了检验产品质量,质量质检员从两台机床的产品中各抽取4件进行测量,结果如下:
| 机床甲 |
10 |
9.8 |
10 |
10.2 |
| 机床乙 |
10.1 |
10 |
9.9 |
10 |
如果你是质量检测员,在收集到上述数据后,你将通过怎样的运算来判断哪台机床生产的零件质量更符合要求.
在某中学举行的数学知识竞赛中,将三个年级参赛学生的成绩在进行整理后分成
5组,绘制出如图所示的频率分布直方图,图中从左到右依次为第一、第二、第三、第四、
第五小组。已知第三小组的频数是15。
(1)求成绩在50—70分的频率是多少;
(2)求这三个年级参赛学生的总人数是多少;
(3)求成绩在80—100分的学生人数是多少;
已知向量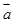 ,
,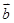 的夹角为
的夹角为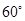 , 且
, 且 ,
,  , 若
, 若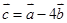 ,
, 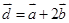 求: (1)
求: (1)  ·
· ; (2)
; (2)  .
.
为了调查甲、乙两个网站受欢迎的程度,随机选取了14天,统计上午8:00—
10:00间各自的点击量,得如下所示的统计图,根据统计图说明: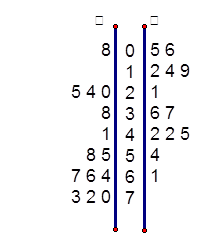
(1)甲、乙两个网站点击量的极差分别是多少?
(2)甲网站点击量在[10,40]间的频率是多少?
(2)甲、乙两个网站哪个更受欢迎?并说明理由。