已知正数数列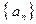 的前
的前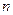 项和为
项和为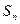 ,
,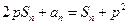
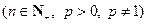 ,数列
,数列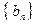 满足
满足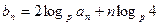 .(Ⅰ)求数列
.(Ⅰ)求数列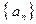 和
和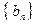 的通项公式; (Ⅱ)当
的通项公式; (Ⅱ)当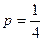 时,
时,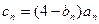 ,求数列
,求数列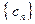 的前
的前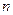 项和
项和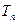 .
.
(本小题满分12分)已知公差不为0的等差数列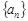 中
中 ,
, 成等比数列,
成等比数列,
(Ⅰ)试求数列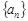 的通项公式;
的通项公式;
(Ⅱ)若数列 满足
满足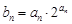 ,试求数列
,试求数列 的前
的前 项和
项和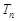 .
.
(本小题满分12分)已知函数 ,
,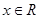 .
.
(Ⅰ)求函数 的单调递增区间;
的单调递增区间;
(Ⅱ)在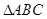 中,角
中,角 所对的边分别是
所对的边分别是 ,若
,若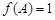 ,
,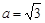
 ,试求
,试求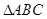 的面积.
的面积.
(本小题满分12分)已知线段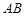 的端点B在圆
的端点B在圆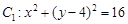 上运动,端点
上运动,端点 的坐标为
的坐标为 ,线段
,线段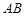 中点为
中点为 ,
,
(Ⅰ)试求 点的轨迹
点的轨迹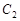 方程;
方程;
(Ⅱ)若圆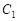 与曲线
与曲线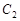 交于
交于 两点,试求线段
两点,试求线段 的长.
的长.
(本小题满分12分)如图,在四棱锥P-ABCD中,PD^平面ABCD,AD=CD,DB平分∠ADC,E为PC的中点.
(Ⅰ)证明:PA∥平面BDE;
(Ⅱ)证明:AC^平面PBD.
(本小题满分12分)在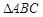 中,
中, ,若点B与点
,若点B与点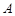 关于直线
关于直线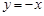 对称,
对称,
(Ⅰ)试求直线 的方程;
的方程;
(Ⅱ)试求线段 的垂直平分线方程.
的垂直平分线方程.