已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,-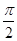 <φ<0)的图象与y轴的交点为(0,1),它在y轴右侧的第一个最高点和第一个最低点的坐标分别为(x0,2)和(x0+2π,-2).
<φ<0)的图象与y轴的交点为(0,1),它在y轴右侧的第一个最高点和第一个最低点的坐标分别为(x0,2)和(x0+2π,-2).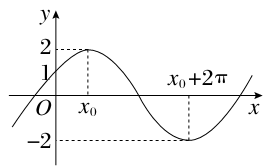
(1)求函数f(x)的解析式;
(2)若锐角θ满足cosθ=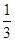 ,求f(2θ)的值.
,求f(2θ)的值.
(本小题满分12分)
如图,平面 ⊥平面
⊥平面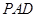 ,
,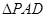 是直角三角形,
是直角三角形, ,四边形
,四边形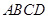 是直角梯形,其中
是直角梯形,其中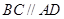 ,
, ,
, ,且
,且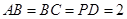 ,
, 是
是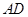 的中点,
的中点,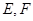 分别是
分别是 的中点.
的中点. 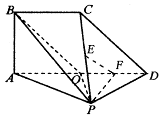
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求二面角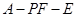 的正切值.
的正切值.
已知数列 是递增数列,且满足
是递增数列,且满足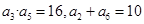 。
。
(1)若 是等差数列,求数列
是等差数列,求数列 的通项公式;
的通项公式;
(2)对于(1)中 ,令
,令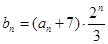 ,求数列
,求数列 的前
的前 项和
项和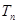 。
。
(本小题满分14分)已知函数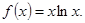
(1)求函数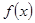 的极值点;
的极值点;
(2)若直线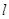 过点(0,—1),并且与曲线
过点(0,—1),并且与曲线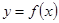 相切,求直线
相切,求直线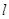 的方程;
的方程;
(3)设函数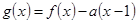 ,其中
,其中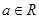 ,求函数
,求函数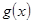 在
在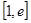 上的最小值.(其中e为自然对数的底数
上的最小值.(其中e为自然对数的底数
(本小题满分12分) 已知椭圆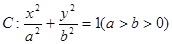 的焦距为
的焦距为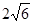 ,椭圆
,椭圆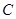 上任意一点到椭圆两个焦点的距离之和为6.
上任意一点到椭圆两个焦点的距离之和为6.
(Ⅰ)求椭圆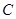 的方程;
的方程;
(Ⅱ)设直线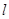
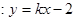 与椭圆
与椭圆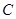 交于
交于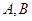 两点,点
两点,点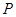 (0,1),且
(0,1),且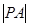 =
=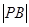 ,求直线
,求直线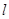 的方程.
的方程.
(本小题满分12分)在几何体ABCDE中,∠BAC=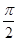 ,DC⊥平面ABC,EB⊥平面ABC,F是BC的中点,AB=AC=BE=2,CD=1
,DC⊥平面ABC,EB⊥平面ABC,F是BC的中点,AB=AC=BE=2,CD=1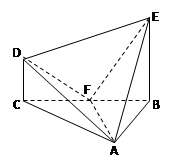
(Ⅰ)求证:DC∥平面ABE;
(Ⅱ)求证:AF⊥平面BCDE;
(Ⅲ)求证:平面AFD⊥平面AFE.