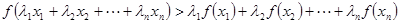设函数f(x)=sin(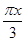 -
-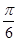 )-2cos2
)-2cos2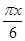 .
.
(1)求y=f(x)的最小正周期及单调递增区间;
(2)若函数y=g(x)与y=f(x)的图象关于直线x=2对称,求当x∈[0,1]时,函数y=g(x)的最大值.
已知函数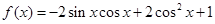
(1)设方程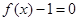 在(0,
在(0,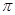 )内有两个零点
)内有两个零点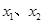 ,求
,求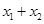 的值;
的值;
(2)若把函数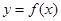 的图像向左移动
的图像向左移动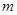
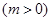 个单位,再向下平移2个单位,使所得函数的图象关于
个单位,再向下平移2个单位,使所得函数的图象关于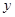 轴对称,求
轴对称,求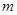 的最小值。
的最小值。
鑫隆房地产公司用2160万元购得一块空地,计划在该地块上建造一栋至少10层、每层2000平方米的楼房.经测算,如果将楼房建为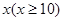 层,则每平方米的平均建筑费用为
层,则每平方米的平均建筑费用为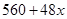 (单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?(注:平均综合费用=平均建筑费用+平均购地费用,平均购地费用=
(单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?(注:平均综合费用=平均建筑费用+平均购地费用,平均购地费用= )
)
在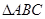 中,设内角
中,设内角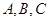 的对边分别为
的对边分别为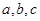 向量
向量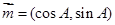 ,向量
,向量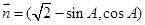 ,若
,若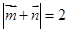
(1)求角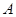 的大小;
的大小;
(2)若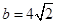 ,且
,且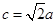 ,求
,求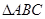 的面积.
的面积.
风景秀美的凤凰湖畔有四棵高大的银杏树,记做A、B、P、Q,欲测量P、Q两棵树和A、P两棵树之间的距离,但湖岸部分地方围有铁丝网不能靠近,现在可以方便的测得A、B两点间的距离为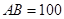 米,如图,同时也能测量出
米,如图,同时也能测量出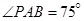 ,
,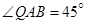 ,
,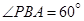 ,
,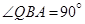 ,则P、Q两棵树和A、P两棵树之间的距离各为多少?
,则P、Q两棵树和A、P两棵树之间的距离各为多少?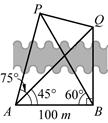
理科已知函数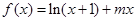 ,当
,当 时,函数
时,函数 取得极大值.
取得极大值.
(Ⅰ)求实数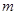 的值;(Ⅱ)已知结论:若函数
的值;(Ⅱ)已知结论:若函数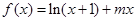 在区间
在区间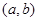 内导数都存在,且
内导数都存在,且 ,则存在
,则存在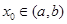 ,使得
,使得 .试用这个结论证明:若
.试用这个结论证明:若 ,函数
,函数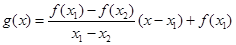 ,则对任意
,则对任意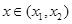 ,都有
,都有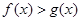 ;(Ⅲ)已知正数
;(Ⅲ)已知正数 满足
满足 求证:当
求证:当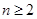 ,
,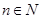 时,对任意大于
时,对任意大于 ,且互不相等的实数
,且互不相等的实数 ,都有
,都有