如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1,M、N分别是A1B、B1C1的中点.
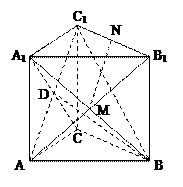
 (Ⅰ)求证:MN⊥平面A1BC;
(Ⅰ)求证:MN⊥平面A1BC;
 (Ⅱ)求直线BC1和平面A1BC所成角的大小.
(Ⅱ)求直线BC1和平面A1BC所成角的大小.


抛物线的顶点在原点,焦点是圆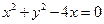 的圆心,(1)求抛物线的方程;(2)直线
的圆心,(1)求抛物线的方程;(2)直线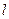 的斜率为
的斜率为 ,且过抛物线的焦点,若
,且过抛物线的焦点,若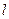 与抛物线、圆依次交于
与抛物线、圆依次交于 四个点,求
四个点,求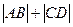 。
。
求顶点在原点,焦点在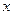 轴上,且截直线
轴上,且截直线 所得的弦长为
所得的弦长为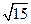 的抛物线的方程。
的抛物线的方程。
已知抛物线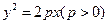 ,过动点
,过动点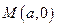 且斜率为
且斜率为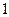 的直线
的直线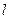 与该抛物线交于不同的两点
与该抛物线交于不同的两点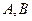 ,
,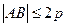 ,(1)求
,(1)求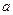 的取值范围;(2)若线段
的取值范围;(2)若线段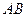 的垂直平分线交
的垂直平分线交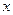 轴于点
轴于点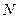 ,求
,求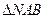 的面积的最大值。
的面积的最大值。
已知函数f(x)在(-1,1)上有定义,f(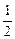 )=-1,当且仅当0<x<1时f(x)<0,且对任意x、y∈(-1,1)都有f(x)+f(y)=f(
)=-1,当且仅当0<x<1时f(x)<0,且对任意x、y∈(-1,1)都有f(x)+f(y)=f(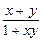 ),试证明:
),试证明:
(1)f(x)为奇函数;(2)f(x)在(-1,1)上单调递减
作出下列函数的图像(1)y=|x-2|(x+1);(2)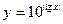 .
.