在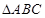 中,角
中,角 、
、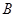 、
、 的对边分别为
的对边分别为 、
、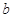 、
、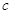 ,且
,且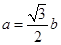 ,
,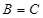 .
.
(Ⅰ)求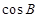 的值;
的值;
(Ⅱ)设函数 ,求
,求 的值.
的值.
设无穷等比数列 的公比为q,且
的公比为q,且 ,
, 表示不超过实数
表示不超过实数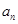 的最大整数(如
的最大整数(如 ),记
),记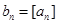 ,数列
,数列 的前
的前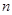 项和为
项和为 ,数列
,数列 的前
的前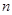 项和为
项和为 .
.
(Ⅰ)若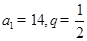 ,求
,求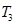 ;
;
(Ⅱ)证明:  (
( )的充分必要条件为
)的充分必要条件为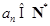 ;
;
(Ⅲ)若对于任意不超过 的正整数n,都有
的正整数n,都有 ,证明:
,证明: .
.
已知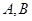 是抛物线
是抛物线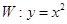 上的两个点,点
上的两个点,点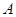 的坐标为
的坐标为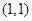 ,直线
,直线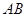 的斜率为
的斜率为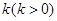 .设抛物线
.设抛物线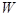 的焦点在直线
的焦点在直线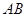 的下方.
的下方.
(Ⅰ)求k的取值范围;
(Ⅱ)设C为W上一点,且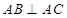 ,过
,过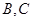 两点分别作W的切线,记两切线的交点为
两点分别作W的切线,记两切线的交点为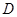 . 判断四边形
. 判断四边形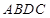 是否为梯形,并说明理由.
是否为梯形,并说明理由.
已知函数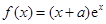 ,其中
,其中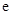 是自然对数的底数,
是自然对数的底数,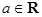 .
.
(Ⅰ)求函数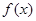 的单调区间;
的单调区间;
(Ⅱ)当 时,求函数
时,求函数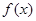 的最小值.
的最小值.
如图,在多面体ABCDEF中,底面ABCD是边长为2的正方形,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,G和H分别是CE和CF的中点.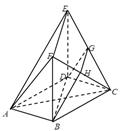
(Ⅰ)求证:AC⊥平面BDEF;
(Ⅱ)求证:平面BDGH//平面AEF;
(Ⅲ)求多面体ABCDEF的体积.