求值: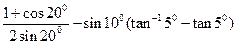
已知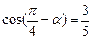 ,
, ,求
,求 的值.
的值.
设函数
(1)证明
(2)设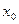 为f(x)的一个极值点,证明
为f(x)的一个极值点,证明
(3)设f(x)在(0,+∞)内的全部极值点按从小到大的顺序排列为a1,a2,…an
证明:
已知方向向量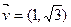 的直线l 过点(
的直线l 过点(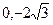 )和椭圆C:
)和椭圆C: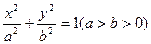 的焦点,且椭圆的中心关于直线l的对称点在椭圆C的右准线上。
的焦点,且椭圆的中心关于直线l的对称点在椭圆C的右准线上。
(1)求椭圆C的方程;
(2)是否存在过点E(-2,0)的直线m交椭圆C于M、N,满足 (O为原点),若存在求出直线的方程,若不存在,请说明理由。
(O为原点),若存在求出直线的方程,若不存在,请说明理由。
已知
(1)判断f(x)的单调性;
(2)设
证明:
(3)证明: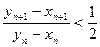
如图,在三棱锥P—ABC中,PA⊥底面ABC,∠BAC=60°,AB=AC=2 ,以PA为直径的球O和PB、PC分别交于B1、C1
,以PA为直径的球O和PB、PC分别交于B1、C1
(1)求证B1C1∥平面ABC
(2)若二面角C—PB—A的大小为arctan2 ,试求球O的表面积。
,试求球O的表面积。