如图5-9所示，半径为R的光滑圆形轨道固定在竖直面内。小球A、B质量分别为m、βm（β为待定系数）。A球从左边与圆心等高处由静止开始沿轨道下滑，与静止于轨道最低点的B球相撞，碰撞后A、B球能达到的最大高度均为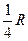
,碰撞中无机械能损失。重力加速度为g。试求：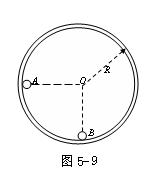
待定系数β;
第一次碰撞刚结束时小球A、B各自的速度和B球对轨道的压力;
小球A、B在轨道最低处第二次碰撞刚结束时各自的速度，并讨论小球A、B在轨道最低处第n次碰撞刚结束时各自的速度。
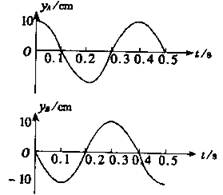
一列简谐横波由质点A向质点B传播。已知A、B两点相距4m，这列波的波长大于2m而小于20m。下图表示在波的传播过程中A、B两质点的振动的图象。求波的传播速度。
、如图，电动传送带以恒定速度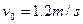
运行，传送带与水平面的夹角
，现将质量m=20kg的物品箱轻放到传送带底端，经过一段时间后，物品箱被送到h=1.8m的平台上，已知物品箱与传送带间的动摩擦因数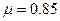
，不计其他损耗，则每件物品箱从传送带底端送到平台上，需要多少时间？每输送一个物品箱，电动机需增加消耗的
|
电能是多少焦耳？（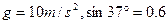
）
A、B两个小球由柔软的细线相连，线长L =" 6m" ,现将A 、B球先后以相同的初速度vo = 4.5m/s，从同一点水平抛出（先A 、后B）相隔时间t0= 0.8s（取g = 10m/s2）。
（1）B球抛出后经多少时间，细线刚好被拉直？(在线拉直前，两球都未落地)
（2）细线刚被拉直时，A 、B球的水平位移（相对于抛出点）各多大？
0如图所示，摩托车演员作特技表演，当到达高台底端时关闭油门，从底端以初速度v0＝20m/s冲上顶部水平的高台，然后从顶部水平飞出(不计空气阻力)，摩托车和人落到缓冲垫上(图中未画出)，摩托车落地速度大小为v＝10 m/s，已知平台顶部距缓冲垫的高度为H＝10 m，g＝10 m/s2。试求摩托车和人飞行的水平距离。(结果取两位有效数字)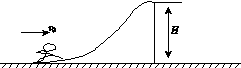
在图中所示的装置中，斜面倾角α=37°，A的质量是m1=10kg，A与B之间的动摩擦因数为μ1=0.1，B的质量为m2=20kg，B与斜面之间的动摩擦因数为μ2=0.2，为使B沿斜面向上匀速运动，应当用多大的力F沿斜面方向向下拉A？
（g取10m/s2,sin37°=0.6,Cos37°=0.8)
