(满分12分)如图,在四棱锥P—ABCD中,PD⊥底面ABCD,底面
ABCD为正方形,PD=DC,E、F分别是AB、PB的中点。
(1)求证:EF⊥CD;
(2)在平面PAD内求一点G,使GF⊥平面PCB,
并证明你的结论;
(3)求DB与平面DEF所成角的大小。
(本小题满分12分)
设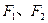 分别为椭圆
分别为椭圆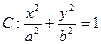 (
( )的左、右焦点,过F2的
)的左、右焦点,过F2的
直线l与椭圆C相交于A、B两点,直线l的倾斜角为600,F1到直线l的
距离为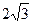 .
.
⑴求椭圆C的焦距;
⑵如果 ,求椭圆C的方程.
,求椭圆C的方程.
(本小题满分12分)
已知函数 的图象在
的图象在 处的切线与
处的切线与 轴平行.
轴平行.
(1)求 与
与 的关系式及f(x)的极大值;
的关系式及f(x)的极大值;
(2)若函数 在区间
在区间 上有最大值为
上有最大值为 ,试求
,试求 的值.
的值.
(本小题满分12分)
如图,由M到N的电路中有4个元件,分别标为T1,T2,T3,T4,电流能通过T1,T2,T3的概率都是p,电流能通过T4的概率是0.9,电流能否通过各元件相互独立.已知T1,T2,T3中至少有一个能通过电流的概率为0.999.
⑴求p;
⑵求电流能在M与N之间通过的概率.
(本小题满分12分)
如图,在四棱锥 中,底面
中,底面 是平行四边形,
是平行四边形, ,且
,且 ,
, ,又
,又 底面
底面 ,
, ,又
,又 为边
为边 上异于
上异于 的点,且
的点,且 .
.
(1)求四棱锥 的体积;
的体积;
(2)求 到平面
到平面 的距离.
的距离.
(本小题满分12分)
记等差数列 的前
的前 项和为
项和为 ,设
,设 ,且
,且 成等比数列,求
成等比数列,求 .
. 