4位参加辩论比赛的同学,比赛规则是:每位同学必须从甲、乙两道题中任选一题做答,选甲题答对得100分,答错得-100分;选乙题答对得90分,答错得-90分.若4位同学的总分为0分,则这4位同学有多少种不同得分情况?
已知函数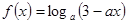
(1)当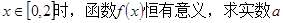 的取值范围;
的取值范围;
(2)是否存在这样的实数 ,使得函数
,使得函数 在区间
在区间 上为减函数,且最大值为1,若存在,求出
上为减函数,且最大值为1,若存在,求出 值;若不存在,说明理由。
值;若不存在,说明理由。
设命题 :实数
:实数 满足
满足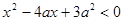 ,其中
,其中 ;命题
;命题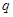 :实数
:实数 满足
满足 且
且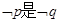 的必要不充分条件,求实数
的必要不充分条件,求实数 的取值范围.
的取值范围.
(本小题满分12分)在数列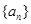 中,
中,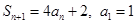 ;
;
(1)设 ,求证数列
,求证数列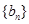 是等比数列;
是等比数列;
(2)设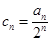 ,求证:数列
,求证:数列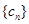 是等差数列;
是等差数列;
(3)求数列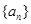 的通项公式及前n项和的公式。
的通项公式及前n项和的公式。
(本小题满分12分)已知 :方程
:方程 表示焦点在
表示焦点在 轴上的双曲线,
轴上的双曲线, :方程
:方程 =(
=( 一
一 )
) 表示开口向右的抛物线.若“
表示开口向右的抛物线.若“

 ”为真命题,“
”为真命题,“

 ”为假命题,求实数
”为假命题,求实数 的范围.
的范围.
(本小题满分12分)点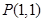 为椭圆
为椭圆 内的一定点,过P点引一直线,与椭圆相交于
内的一定点,过P点引一直线,与椭圆相交于 两点,且P恰好为弦AB的中点,如图所示,求弦AB所在的直线方程及弦AB的长度。
两点,且P恰好为弦AB的中点,如图所示,求弦AB所在的直线方程及弦AB的长度。