如图所示:小圆圈表示网络的结点,结点之间的连线表示它们有网络联系,连线上标注的数字表示该段网线单位时间内可以通过的最大信息量,现从结点A向结点B传递信息,信息可以分开沿不同路线同时传递,求单位时间内传递的最大信息量.
如图，将圆分成n个区域，用3种不同颜色给每一个区域染色，要求相邻区域颜色互异，把不同的染色方法种数记为
。求
（1）
及与
的关系式；
（2）数列
的通项公式，并证明：
如图，正四棱锥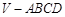
的底面边长为2a，高为h. 以其底面中心O为坐标原点建立空间直角坐标系
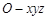，其中Ox//BC，Oy//AB，E为VC的中点.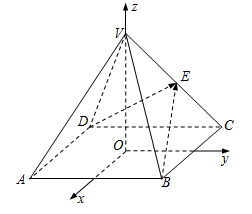
（1）用a和h表示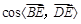
；
（2）当
是二面角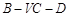
的平面角时，求cos
选修4—5：不等式选讲
设函数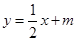
．
（1）当
时，求函数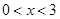
的定义域；
（2）若函数
的定义域为R，试求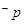
的取值范围．
选修4—4：坐标系与参数方程
在平面直角坐标系xOy中，以O为极点，Ox为极轴建立极坐标系，且两种坐标系长度单位一致. 已知直线l的极坐标方程为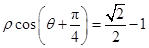
，圆C在直角坐标系中的参数方程为
（
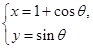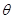为参数），求直线l与圆C的公共点的个数.
（本小题满分14分）如图，在正三棱柱ABC－A1B1C1中，D、E分别为CC1、A1B1的中点．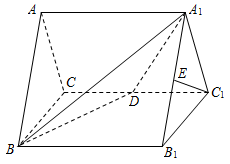
求证：C1E∥平面A1BD；
（2）求证：平面ABB1A1⊥平面A1BD.