已知甲盒内有大小相同的1个红球和3个黑球,乙盒内有大小相同的2个红球和4个黑球.现从甲、乙两个盒内各任取2个球.
(Ⅰ)求取出的4个球均为黑球的概率;
(Ⅱ)求取出的4个球中恰有1个红球的概率;
(Ⅲ)设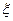 为取出的4个球中红球的个数,求
为取出的4个球中红球的个数,求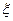 的分布列和数学期望.
的分布列和数学期望.
在平面直角坐标系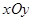 中,与向量
中,与向量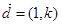 平行的直线
平行的直线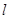 经过椭圆
经过椭圆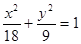 的右焦点
的右焦点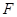 ,与椭圆相交于
,与椭圆相交于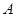 、
、 两点.
两点.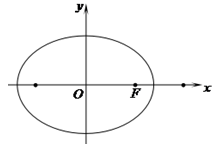
(1)若点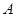 在
在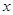 轴的上方,且
轴的上方,且 ,求直线
,求直线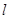 的方程;
的方程;
(2)若 ,
,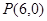 ,求△
,求△ 的面积;
的面积;
(3)当 (
(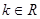 且
且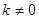 )变化时,是否存在一点
)变化时,是否存在一点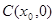 ,使得直线
,使得直线 和
和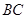 的斜率之和为
的斜率之和为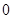 .若存在,请证明结论;若不存在,请说明理由.
.若存在,请证明结论;若不存在,请说明理由.
已知⊙M:x2+(y-2)2=1,Q是x轴上的动点,QA,QB分别切⊙M于A,B两点.
(1)若|AB|= ,求|MQ|、Q点的坐标以及直线MQ的方程;
,求|MQ|、Q点的坐标以及直线MQ的方程;
(2)求证:直线AB恒过定点.
选修4-5:不等式选讲
已知函数 .
.
(1)当 时,解不等式
时,解不等式 ;
;
(2)若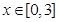 时,
时, ,求实数
,求实数 的取值范围.
的取值范围.
选修4-4:坐标系与参数方程
已知曲线 的极坐标方程是
的极坐标方程是 ,以极点为原点,极轴为
,以极点为原点,极轴为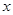 轴的正半轴建立平面直角坐标系,直线
轴的正半轴建立平面直角坐标系,直线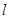 的参数方程为
的参数方程为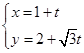 (
(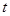 为参数),
为参数),
(1)写出直线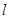 的普通方程与曲线
的普通方程与曲线 的直角坐标方程;
的直角坐标方程;
(2)设曲线 经过伸缩变换
经过伸缩变换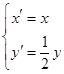 后得到曲线
后得到曲线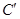 ,设
,设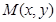 为
为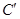 上任意一点,求
上任意一点,求 的最小值,并求相应的点
的最小值,并求相应的点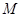 的坐标.
的坐标.
几何证明选讲
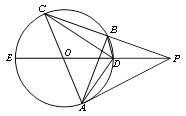
如图,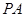 是
是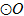 的切线,
的切线, 过圆心
过圆心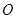 ,
,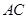 为
为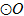 的直径,
的直径,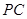 与
与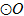 相交于
相交于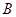 、
、 两点,连结
两点,连结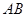 、
、 .
.
(1)求证: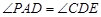 ;
;
(2)求证: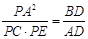 .
.