如图,面积为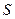 的正方形
的正方形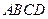 中有一个不规则的图形
中有一个不规则的图形 ,可按下面方法估计
,可按下面方法估计 的面积:在正方形
的面积:在正方形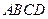 中随机投掷
中随机投掷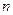 个点,若
个点,若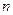 个点中有
个点中有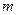 个点落入
个点落入 中,则
中,则 的面积的估计值为
的面积的估计值为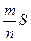 ,假设正方形
,假设正方形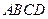 的边长为2,
的边长为2, 的面积为1,并向正方形
的面积为1,并向正方形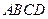 中随机投掷
中随机投掷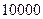 个点,以
个点,以 表示落入
表示落入 中的点的数目.
中的点的数目.
(I)求 的均值
的均值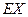 ;
;
(II)求用以上方法估计 的面积时,
的面积时, 的面积的估计值与实际值之差在区间
的面积的估计值与实际值之差在区间 内的概率.
内的概率.
附表: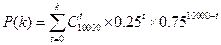
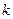 |
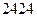 |
 |
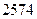 |
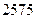 |
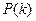 |
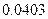 |
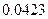 |
 |
 |
已知函数f(x)=cos(2x- )+sin2x-cos2x.
)+sin2x-cos2x.
(Ⅰ)求函数f(x)的最小正周期及其图象的对称轴方程;
(Ⅱ)设函数g(x)=[f(x)]2+f(x),求g(x)的值域.
已知函数 .
.
(Ⅰ)请写出函数 在每段区间上的解析式,并在图中的直角坐标系中作出函数
在每段区间上的解析式,并在图中的直角坐标系中作出函数 的图象;
的图象;
(II)若不等式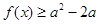 对任意的实数
对任意的实数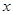 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
已知在直角坐标系 中,曲线
中,曲线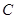 的参数方程为:
的参数方程为: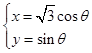 (
(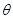 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系 取相同的长度单位,且以原点
取相同的长度单位,且以原点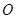 为极点,以
为极点,以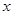 轴正半轴为极轴)中,直线
轴正半轴为极轴)中,直线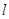 的极坐标方程为:
的极坐标方程为: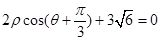 .
.
(Ⅰ)写出曲线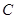 和直线
和直线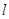 在直角坐标系下的方程;
在直角坐标系下的方程;
(II)设点 是曲线
是曲线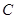 上的一个动点,求它到直线
上的一个动点,求它到直线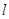 的距离的最小值.
的距离的最小值.
如图, 是圆的内接四边形,
是圆的内接四边形,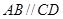 ,过
,过 点的圆的切线与
点的圆的切线与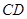 的延长线交于
的延长线交于 点,证明:
点,证明:
(Ⅰ)
(II)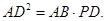

已知函数
(I)求函数 的最小值;
的最小值;
(II)对于函数 和
和 定义域内的任意实数
定义域内的任意实数 ,若存在常数
,若存在常数 ,使得不等式
,使得不等式 和
和 都成立,则称直线
都成立,则称直线 是函数
是函数 和
和 的“分界线”.
的“分界线”.
设函数 ,
,
 ,试问函数
,试问函数 和
和 是否存在“分界线”?若存在,求出“分界线”的方程.若不存在请说明理由.
是否存在“分界线”?若存在,求出“分界线”的方程.若不存在请说明理由.