已知f(x)=ln(1+x2)+ax(a≤0)。
（1）讨论f(x)的单调性。
（2）证明：（1+
）（1+
）…（1+
）＜e （n∈N*，n≥2,其中无理数e=2.71828…）
（（本小题满分14分）
已知
。
（1）若函数
为奇函数，求实数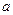
的值；
（2）若函数在区间
上是增函数，求实数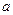的值组成的集合A；
（3）设关于
的方程
的两个非零实根为
，试问：是否存在实数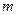
，使得不等式
对任意
及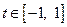
恒成立？若存在，求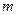的取值范围；若不存在，请说明理由。
（本小题满分12分）
如图，正方形ABCD所在平面与平面四边形ABEF所在平面互相垂直，⊿ABE是等腰直角三角形，AB=AE，FA=FE，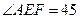
°
（1）求证：EF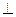
平面BCE；
（2）求二面角
的大小。
（本小题满分12分）
扇形
中，半径
°，在
的延长线上有一动点
，过点作
与半圆弧
相切于点
，且与过点
所作的
的垂线交于点
，此时显然有CO=CD，DB=DE，问当OC多长时，直角梯形
面积最小，并求出这个最小值。
（（本小题满分12分）
如图所示，已知三棱柱
，在某个空间直角坐标系中，
，
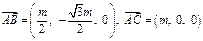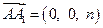，其中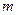
、
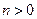
（1）证明：三棱柱是正三棱柱；
（2）若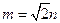
，求直线
与平面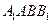
所成角的大小。
（本小题满分12分）
设函数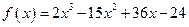
.
（1）求函数的极值和单调区间；
（2）求函数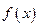
在区间
上的最大值和最小值。