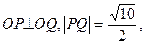
已知数列{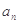 }的前n项和为
}的前n项和为 ,且满足
,且满足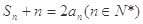 .
.
(1)证明:数列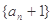 为等比数列,并求数列{
为等比数列,并求数列{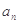 }的通项公式;
}的通项公式;
(2)数列{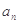 }满足
}满足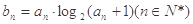 ,其前n项和为
,其前n项和为 ,试求满足
,试求满足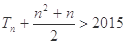 的最小正整数n.
的最小正整数n.
设函数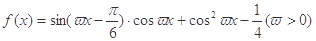 图像上的一个最高点为A,其相邻的一个最低点为B,且|AB|=
图像上的一个最高点为A,其相邻的一个最低点为B,且|AB|=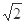 .
.
(1)求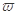 的值;
的值;
(2)设△ABC的内角A、B、C的对边分别为a、b、c,且b+c=2,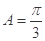 ,求
,求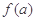
的值域.
已知函数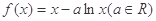
(1)当a=2时,求曲线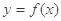 在点A(1,f(1))处的切线方程;
在点A(1,f(1))处的切线方程;
(2)讨论函数f(x)的单调性与极值.
某中学高二年级的甲、乙两个班中,需根据某次数学预赛成绩选出某班的5名学生参加数学竞赛决赛,已知这次预赛他们取得的成绩(满分100分)的茎叶图如图所示,其中甲班5名学生成绩的平均分是83,乙班5名学生成绩的中位数是86.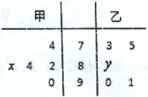
(1)求出x,y的值,且分别求甲、乙两个班中5名学生成绩的方差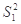 、
、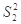 ,并根据结
,并根据结
果,你认为应该选派哪一个班的学生参加决赛?
(2)从成绩在85分及以上的学生中随机抽取2名.求至少有1名来自甲班的概率.
等差数列{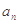 }足:
}足: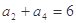 ,
,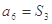 ,其中
,其中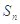 为数列{
为数列{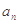 }前n项和.
}前n项和.
(1)求数列{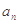 }通项公式;
}通项公式;
(2)若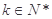 ,且
,且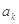 ,
, ,
,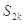 成等比数列,求k值.
成等比数列,求k值.