某中学高二年级的甲、乙两个班中，需根据某次数学预赛成绩选出某班的5名学生参加数学竞赛决赛，已知这次预赛他们取得的成绩（满分100分）的茎叶图如图所示，其中甲班5名学生成绩的平均分是83，乙班5名学生成绩的中位数是86．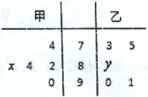
（1）求出x，y的值，且分别求甲、乙两个班中5名学生成绩的方差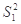
、
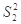，并根据结
果，你认为应该选派哪一个班的学生参加决赛？
（2）从成绩在85分及以上的学生中随机抽取2名．求至少有1名来自甲班的概率．
如图所示,AB为☉O直径,直线CD与☉O相切于E,AD垂直CD于D,BC垂直CD于C,EF垂直AB于F,连接AE,BE.证明: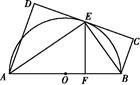
(1)∠FEB=∠CEB;
(2)EF2=AD·BC.
如图,直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于点E,DB垂直BE交圆于点D.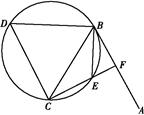
(1)证明:DB=DC;
(2)设圆的半径为1,BC=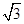
,延长CE交AB于点F,求△BCF外接圆的半径.
如图,☉O和☉O′相交于A,B两点,过A作两圆的切线分别交两圆于C、D两点,连结DB并延长交☉O于点E.证明: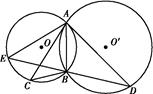
(1)AC·BD=AD·AB;
(2)AC=AE.
设函数f(x)=xn+bx+c(n∈N+,b,c∈R).
(1)设n≥2,b=1,c=-1,证明:f(x)在区间(
,1)内存在唯一零点;
(2)设n为偶数,|f(-1)|≤1,|f(1)|≤1,求b+3c的最小值和最大值;
(3)设n=2,若对任意x1,x2∈[-1,1],有|f(x1)-f(x2)|≤4,求b的取值范围.
已知函数f(x)对任意实数x均有f(x)=kf(x+2),其中常数k为负数,且f (x)在区间[0,2]上有表达式f(x)=x(x-2).
(1)求f(-1),f(2.5)的值;
(2)写出f(x)在[-3,3]上的表达式,并讨论函数f(x)在[-3,3]上的单调性;
(3)求出f(x)在[-3,3]上的最小值与最大值,并求出相应的自变量的取值.