(本小题满分12分)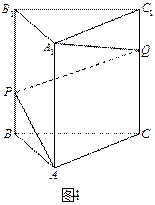 如图4,正三棱柱
如图4,正三棱柱 中,
中, ,
, 、
、 分别是侧棱
分别是侧棱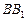 、
、 上的点,且使得折线
上的点,且使得折线 的长
的长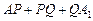 最短.
最短.
(1)证明:平面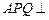 平面
平面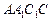 ;(2)求直线
;(2)求直线 与平面
与平面 所成角的余弦值.
所成角的余弦值.
(本小题14分)
已知椭圆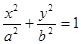 (
(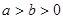 )过点
)过点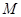 (0,2),离心率
(0,2),离心率 .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)设过定点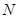 (2,0)的直线
(2,0)的直线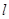 与椭圆相交于
与椭圆相交于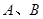 两点,且
两点,且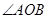 为锐角(其中
为锐角(其中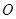 为坐标原点),求直线
为坐标原点),求直线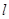 斜率的取值范围.
斜率的取值范围.
(本小题满分13分)
已知函数
(I)若曲线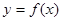 在点
在点 处的切线与直线
处的切线与直线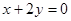 垂直,求a的值;
垂直,求a的值;
(II)求函数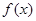 的单调区间;
的单调区间;
(满分13分)
如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且△PMB为正三角形.
(1)求证:DM∥平面APC;
(2)求证:平面ABC⊥平面APC;
(满分13分)
(1)某三棱锥的侧视图和俯视图如图所示,求三棱锥的体积.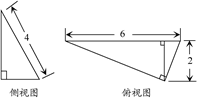
(2)过直角坐标平面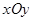 中的抛物线
中的抛物线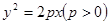 的焦点
的焦点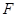 作一条倾斜角为
作一条倾斜角为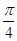 的直线与抛物线相交于A,B两点. 用
的直线与抛物线相交于A,B两点. 用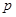 表示A,B之间的距离;
表示A,B之间的距离;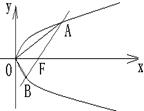
(满分12分)已知函数 .
.
(1)求函数 的最小正周期和最大值;
的最小正周期和最大值;
(2)求函数 在区间
在区间 上的最大值与最小值.
上的最大值与最小值.