设椭圆 :
: 的离心率为
的离心率为 ,点
,点 (
(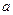 ,0),
,0), (0,
(0, ),原点
),原点 到直线
到直线 的距离为
的距离为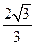 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设点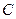 为(
为(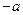 ,0),点
,0),点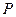 在椭圆
在椭圆 上(与
上(与 、
、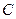 均不重合),点
均不重合),点 在直线
在直线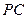 上,若直线
上,若直线 的方程为
的方程为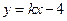 ,且
,且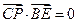 ,试求直线
,试求直线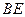 的方程.
的方程.
((本小题满分12分)甲与乙进行一场乒乓球单打比赛时,甲获胜的局数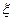 的期望
的期望 ,每场比赛打满3局。(I)甲、乙进行一场比赛,通过计算填写下表(不必书写计算过程);
,每场比赛打满3局。(I)甲、乙进行一场比赛,通过计算填写下表(不必书写计算过程);
| 甲获胜的局数 |
0 |
1 |
2 |
3 |
| 3相应的概率 |
(II)求在三场比赛中,至少有两场比赛甲胜1局或2局的概率。
(本小题满分10分)已知函数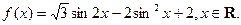
(I)求函数 的最大值及对应的x的取值集合;
的最大值及对应的x的取值集合;
|
(II)在给定的坐标系中,画出函数 上的图象。
上的图象。
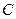

(1)试求 的值,使圆
的值,使圆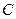 的面积最小;
的面积最小;
(2)求与满足(1)中条件的圆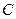 相切,且过点
相切,且过点 的直线方程.
的直线方程.
(1)在图5给定的直角坐标系内画出 的图象;
的图象;
(2)写出 的单调递增区间.
的单调递增区间.


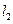

(1)直线 与
与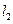 的交点
的交点 的坐标;(2)过点
的坐标;(2)过点 且与
且与 垂直的直线方程
垂直的直线方程