袋中共有10个大小相同的编号为1、2、3的球，其中1号球有1-优题课

题文

袋中共有10个大小相同的编号为1、2、3的球，其中1号球有1个，2号球有3个，3号球有6个．
（1）从袋中任意摸出2个球，求恰好是一个2号球和一个3号球的概率；
（2）从袋中任意摸出2个球，记得到小球的编号数之和为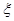，求随机变量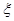的分布列和数学期望．

科目数学题型解答题难度中等

知识点：随机思想的发展

登录免费查看答案和解析

相关试题

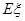已知向量 $a = (\sin θ, - 2)$ 与 $b = (1, \cos θ)$ 互相垂直，其中 $θ \in (0, \frac{π}{2})$ ,
（1）求 $\sin θ$ 和 $\cos θ$ 的值
（2）若 $5 \cos (θ - φ) = 3 \sqrt{5} \cos φ$ ， $0 < φ < \frac{π}{2}$ ,求 $\cos φ$ 的值.

已知函数 $f (x) = \sin (ω x + φ)$ 其中 $ω > 0$ ， $|φ| < \frac{π}{2}$ ,
（1）若 $\cos \frac{π}{4} \cos φ - \sin \frac{3 π}{4} \sin φ = 0$ ,求 $φ$ 的值；
（2）在（1）的条件下，若函数 $f (x)$ 的图象的相邻两条对称轴之间的距离等于 $\frac{π}{3}$ ，求函数 $f (x)$ 的解析式；并求最小正实数 $m$ ，使得函数 $f (x)$ 的图象向左平移 $m$ 个单位所对应的函数是偶函数.

（已知函数.
(Ⅰ) 若数列{a_n}的首项为a₁=1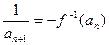，(nÎN₊)，求{a_n}的通项公式a_n；
(Ⅱ) 设b_n=a_n₊₁²+a_n₊₂²+¼+a_2n+1²，是否存在最小的正整数k，使对于任意nÎN₊有b_n<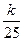成立.若存在，求出k的值；若不存在，说明理由.

（（ 12分）如图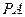，垂直于矩形所在的平面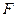，，，、分别是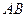、的中点。（1）求证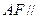：平面；
（2）求证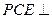：平面平面；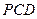
（3）求二面角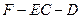的大小.

（(12分)大学毕业生小明到甲、乙、丙三个单位应聘，其被录用的概率分别为（各单位是否录用他相互独立，允许小明被多个单位同时录用）（1）求小明没有被录用的概率；（2）设录用小明的单位个数为，求的分布列和它的数学期望。

试卷网试题网古诗词网作文网范文网

Copyright ©2020-2025 优题课 youtike.com 版权所有

粤ICP备20024846号