((12分)大学毕业生小明到甲、乙、丙三个单位应聘,其被录用的概率分别为 (各单位是否录用他相互独立,允许小明被多个单位同时录用) (1)求小明没有被录用的概率;(2)设录用小明的单位个数为
(各单位是否录用他相互独立,允许小明被多个单位同时录用) (1)求小明没有被录用的概率;(2)设录用小明的单位个数为 ,求
,求 的分布列和它的数学期望。
的分布列和它的数学期望。
从数列 中抽出一些项,依原来的顺序组成的新数列叫数列
中抽出一些项,依原来的顺序组成的新数列叫数列 的一个子列.
的一个子列.
(1)写出数列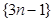 的一个是等比数列的子列;
的一个是等比数列的子列;
(2)若 是无穷等比数列,首项
是无穷等比数列,首项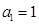 ,公比
,公比 且
且 ,则数列
,则数列 是否存在一个子列
是否存在一个子列
为无穷等差数列?若存在,写出该子列的通项公式;若不存在,证明你的结论.
如图,已知椭圆E: 的离心率为
的离心率为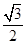 ,过左焦点
,过左焦点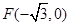 且斜率为
且斜率为 的直线交椭圆E于A,B两点,线段AB的中点为M,直线
的直线交椭圆E于A,B两点,线段AB的中点为M,直线 :
: 交椭圆E于C,D两点.
交椭圆E于C,D两点.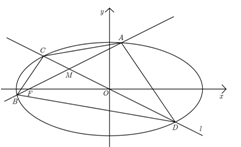
(1)求椭圆E的方程;
(2)求证:点M在直线 上;
上;
(3)是否存在实数k,使得三角形BDM的面积是三角形ACM的3倍?若存在,求出k的值;
若不存在,说明理由.
已知曲线
 .
.
(1)求曲线在点( )处的切线方程;
)处的切线方程;
(2)若存在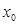 使得
使得 ,求
,求 的取值范围.
的取值范围.
如图,在棱长为1的正方体ABCD-A1B1C1D1中,点E是棱AB上的动点.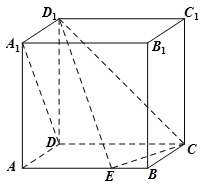
(1)求证:DA1⊥ED1;
(2)若直线DA1与平面CED1成角为45o,求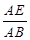 的值;
的值;
(3)写出点E到直线D1C距离的最大值及此时点E的位置(结论不要求证明).
年龄在60岁(含60岁)以上的人称为老龄人,某地区老龄人共有35万,随机调查了该地区700名老龄人的健康状况,结果如下表:
| 健康指数 |
2 |
1 |
0 |
-1 |
| 60岁至79岁的人数 |
250 |
260 |
65 |
25 |
| 80岁及以上的人数 |
20 |
45 |
20 |
15 |
其中健康指数的含义是:2表示“健康”,1表示“基本健康”,0表示“不健康,但生活能够自理”,-1表示“生活不能自理”。
(1)估计该地区80岁以下老龄人生活能够自理的概率。
(2)若一个地区老龄人健康指数的平均值不小于1.2,则该地区可被评为“老龄健康地区”.
请写出该地区老龄人健康指数X分布列,并判断该地区能否被评为“老龄健康地区”.