.(本小题满分12分)
为了解某校高三学生质检数学成绩分布,从该校参加质检的学生数学成绩中抽取一个样本,并分成5组,绘成如图所示的频率分布直方图.若第一组至第五组数据的频率之比为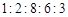 ,最后一组数据的频数是6.
,最后一组数据的频数是6.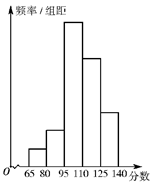
(Ⅰ)估计该校高三学生质检数学成绩在125~140分之间的概率,并求出样本容量;
(Ⅱ)从样本中成绩在65~95分之间的学生中任选两人,求至少有一人成绩在65~80分之间的概率.
已知函数 的定义域为[0,1],求函数
的定义域为[0,1],求函数 的定义域.
的定义域.
(本小题满分12分)已知动点M到点A(2,0)的距离是它到点B(8,0)的距离的一半,求:
(1) 动点M的轨迹方程;
(2) 若N为线段AM的中点,试求点N的轨迹.
(本小题满分12分)已知圆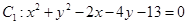 与圆
与圆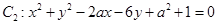 (其中
(其中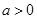 ) 相外切,且直线
) 相外切,且直线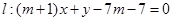 与圆
与圆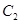 相切,求
相切,求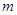 的值.
的值.
(本小题满分12分)已知圆C: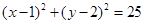 ,直线L:
,直线L: 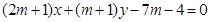
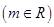
(1) 证明:无论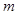 取什么实数,L与圆恒交于两点;
取什么实数,L与圆恒交于两点;
(2) 求直线被圆C截得的弦长最小时直线L的斜截式方程.
(本小题满分12分)如图,在正方体ABCD-A1B1C1D1中,E、F为棱AD、AB的中点.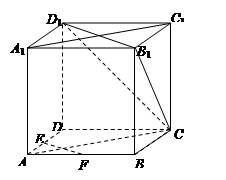
(1)求证:EF ∥平面CB1D1;
(2)求证:平面CAA1C1⊥平面CB1D1.