(本小题满分12分)如图,在正方体ABCD-A1B1C1D1中,E、F为棱AD、AB的中点.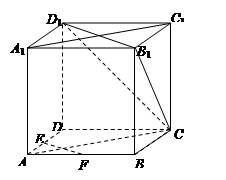
(1)求证:EF ∥平面CB1D1;
(2)求证:平面CAA1C1⊥平面CB1D1.
已知函数 (a,b均为正常数).
(a,b均为正常数).
(1)求证:函数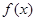 在
在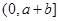 内至少有一个零点;
内至少有一个零点;
(2)设函数在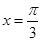 处有极值,
处有极值,
①对于一切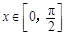 ,不等式
,不等式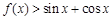 恒成立,求
恒成立,求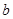 的取值范围;
的取值范围;
②若函数f(x)在区间 上是单调增函数,求实数
上是单调增函数,求实数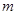 的取值范围.
的取值范围.
如图,在半径为 、圆心角为60°的扇形的
、圆心角为60°的扇形的 弧上任取一点
弧上任取一点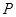 ,作扇形的内接矩形
,作扇形的内接矩形 ,使点
,使点 在
在 上,点
上,点 在
在 上,设矩形
上,设矩形 的面积为
的面积为 .
.
(Ⅰ) 按下列要求写出函数关系式:
① 设 ,将
,将 表示成
表示成 的函数关系式;
的函数关系式;
② 设 ,将
,将 表示成
表示成 的函数关系式.
的函数关系式.
(Ⅱ) 请你选用(Ⅰ)中的一个函数关系式,求 的最大值.
的最大值.
在△ABC中,角A,B,C的对边分别为a,b,c,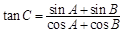 .
.
(1)求角C的大小;
(2)若△ABC的外接圆直径为1,求 的取值范围.
的取值范围.
在△ 中,角
中,角 、
、 、
、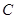 所对的边分别为
所对的边分别为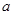 、
、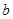 、
、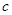 ,且
,且 .
.
(Ⅰ)若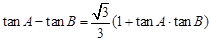 ,求角
,求角 ;
;
(Ⅱ)设 ,
, ,试求
,试求 的最大值.
的最大值.
已知 是同一平面内的三个向量,其中
是同一平面内的三个向量,其中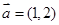
(1)若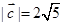 ,且
,且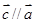 ,求:
,求: 的坐标
的坐标
(2)若 ,且
,且 与
与 垂直,求
垂直,求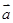 与
与 的夹角
的夹角