已知函数 ,当
,当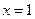 时,有极大值
时,有极大值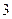 ;
;
(1)求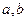 的值;(2)求函数
的值;(2)求函数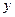 的极小值。
的极小值。
已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点.
(1)证明: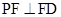 ;
;
(2)判断并说明PA上是否存在点G,使得EG∥平面PFD;
(3)若PB与平面ABCD所成的角为45°,求二面角A-PD-F的平面角的余弦值.
已知命题p:x1和x2是方程 的两个实根,不等式
的两个实根,不等式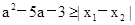 对任意实数
对任意实数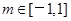 恒成立;命题q:不等式
恒成立;命题q:不等式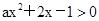 有解,若命题p是真命题,命题q是假命题,求a的取值范围.
有解,若命题p是真命题,命题q是假命题,求a的取值范围.
“地沟油”严重危害了人民群众的身体健康,某企业在政府部门的支持下,进行技术攻关,新上了一种从“食品残渣”中提炼出生物柴油的项目,经测算,该项目月处理成本y(元)与月处理量x(吨)之间的函数关系可以近似的表示为: 且每处理一吨“食品残渣”,可得到能利用的生物柴油价值为200元,若该项目不获利,政府将补贴.
且每处理一吨“食品残渣”,可得到能利用的生物柴油价值为200元,若该项目不获利,政府将补贴.
(1)当x∈[200,300]时,判断该项目能否获利?如果获利,求出最大利润;如果不获利,则政府每月至少需要补贴多少元才能使该项目不亏损.
(2)该项目每月处理量为多少吨时,才能使每吨的平均处理成本最低?
已知函数f(x)=cos(2x+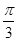 )+sin2x
)+sin2x
(1)求函数f(x)的单调递减区间及最小正周期;
(2)设锐角△ABC的三内角A,B,C的对边分别是a,b,c,若c= ,cosB=
,cosB= ,f(
,f(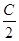 )=-
)=-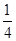 ,求b.
,求b.
项数为n的数列a1,a2,a3, ,an的前k项和为Sk(k=1,2,3, ,n),定义 为该项数列的“凯森和”,如果项数为
为该项数列的“凯森和”,如果项数为 项的数列
项的数列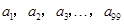 的 “凯森和”为
的 “凯森和”为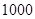 ,那么项数为100的数列100,
,那么项数为100的数列100,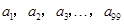 的“凯森和”为( )
的“凯森和”为( )
| A.991 | B.1 001 | C.1 090 | D.1 100 |