已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点.
(1)证明: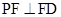 ;
;
(2)判断并说明PA上是否存在点G,使得EG∥平面PFD;
(3)若PB与平面ABCD所成的角为45°,求二面角A-PD-F的平面角的余弦值.
(本小题满分12分)
椭圆 与直线
与直线 相交于
相交于 、
、 两点,且
两点,且 (
( 为坐标原点).(Ⅰ)求证:
为坐标原点).(Ⅰ)求证: 等于定值;
等于定值;
(Ⅱ)当椭圆的离心率 时,求椭圆长轴长的取值范围.
时,求椭圆长轴长的取值范围.
(本小题满分12分)
如图,在三棱柱 中,所有的棱长都为2,
中,所有的棱长都为2, .
.
(Ⅰ)求证: ;
;
(Ⅱ)当三棱柱 的体积最大时,求平面
的体积最大时,求平面 与平面
与平面 所成的锐角的余弦值.
所成的锐角的余弦值.
(本小题满分12分)
某甲有一个放有3个红球、2个白球、1个黄球共6个球的箱子;某乙也有一个放有3个红球、2个白球、1个黄球共6个球的箱子.
(Ⅰ)若甲在自己的箱子里任意取球,取后不放回,每次只取一个球,直到取到红球为止,求甲取球次数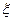 的数学期望;
的数学期望;
(Ⅱ)若甲、乙两人各从自己的箱子里任取一球比颜色,规定同色时为甲胜,异色时为乙胜,这个游戏规则公平吗?请说明理由.
在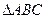 中,
中,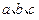 分别为角
分别为角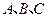 的对边,且满足
的对边,且满足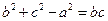 .
.
(Ⅰ)求角 的值;
的值;
(Ⅱ)若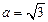 ,设角
,设角 的大小为
的大小为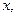
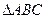 的周长为
的周长为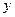 ,求
,求 的最大值.
的最大值.
设函数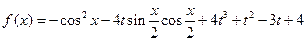 ,
, ,其中
,其中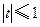 ,将
,将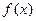 的最小值记为
的最小值记为 .
.
(1)求 的表达式;
的表达式;
(2)讨论 在区间
在区间 内的单调性并求极值.
内的单调性并求极值.