在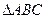 中,
中,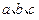 分别为角
分别为角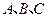 的对边,且满足
的对边,且满足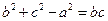 .
.
(Ⅰ)求角 的值;
的值;
(Ⅱ)若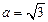 ,设角
,设角 的大小为
的大小为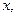
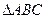 的周长为
的周长为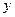 ,求
,求 的最大值.
的最大值.
(本小题满分13分)
从5个男生,4个女生中选3人参加课外活动。
(1)求男生甲必须参加的概率。
(2)求男女生至少都有一名的选法有多少种。(注:结果用数字作答)
(本小题共12分)(注意:在试题卷上作答无效)
已知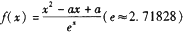
(1)求 的单调区间;
的单调区间;
(2)设 ’若存在
’若存在 使得
使得 成的取值范围.
成的取值范围.
(本小题共12分)(注意:在试题卷上作答无效)
已知数列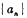 中,
中, ,点
,点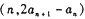 在直线y = x上,其中n = 1,2,3,….
在直线y = x上,其中n = 1,2,3,….
(1) 令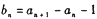 ,证明数列
,证明数列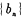 是等比数列;
是等比数列;
(2) 设 分别为数列
分别为数列 的前n项和,证明数列
的前n项和,证明数列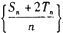 是等差数列
是等差数列
(本小题共12分)(注意:在试题卷上作答无效)
已知抛物线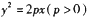 上一动点P,抛物线内一点A(3,2) ,F为焦点且
上一动点P,抛物线内一点A(3,2) ,F为焦点且 的最小值为
的最小值为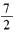 .
.
(1)求抛物线的方程以 及使得
及使得 取最小值时的P点坐标;
取最小值时的P点坐标;
(2)过(1)中的P点作两条互相垂直的直线与抛物线分别交于C、D两点,直线CD是否过一定点?若是,求出该定点的坐标,若不是,请说明理由.
(本小题共12分)(注意:在试题卷上作答无效) 如图,四棱锥S -ABCD
如图,四棱锥S -ABCD 的底面是边长为3的正方形,SD丄底面ABCD,SB=
的底面是边长为3的正方形,SD丄底面ABCD,SB= ,点E、G分别在AB、SC上,且
,点E、G分别在AB、SC上,且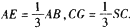
(1) 证明:BC//平面SDE;
(2) 求面SAD与面SBC所成二面角的大小.