(本小题共12分）（注意:在试题卷上作答无效）
已知抛物线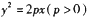
上一动点P，抛物线内一点A(3,2) ,F为焦点且
的最小值为
.
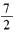(1)求抛物线的方程以
及使得
取最小值时的P点坐标；
(2)过（1)中的P点作两条互相垂直的直线与抛物线分别交于C、D两点，直线CD是否过一定点？若是，求出该定点的坐标,若不是，请说明理由.
棱长为2的正方体
中，E为
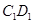的中点.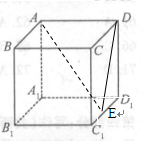
（1）求证：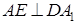
；
（2）求异面直线AE与
所成的角的正弦值.
已知直线L经过点
，且直线L在x轴上的截距等于在y轴上的截距的2倍，求直线L的方程.
已知函数
，
．
（1）若
，判断函数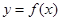
的奇偶性，并加以证明；
（2）若函数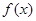
在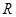
上是增函数，求实数
的取值范围；
（3）若存在实数
使得关于
的方程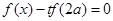
有三个不相等的实数根，求实数
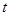的取值范围．
我国加入WTO后，根据达成的协议，若干年内某产品关税与市场供应量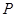
的关系允许近似的满足：
（其中
为关税的税率，且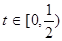
，
为市场价格，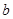
、
为正常数），当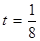
时的市场供应量曲线如图：
（1）根据图象求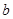、的值；
（2）若市场需求量为
，它近似满足
．当
时的市场价格称为市场平衡价格．为使市场平衡价格控制在不低于9元，求税率的最小值．
已知函数
且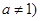
的图象经过点
．
（1）求函数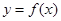
的解析式；
（2）设
，用函数单调性的定义证明：函数
在区间
上单调递减；
（3）解不等式：
．