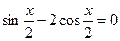 .
.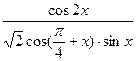 的值.
的值.
(本小题满分12分)
已知函数 R).
R).
(Ⅰ)若a=1,函数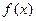 的图象能否总在直线
的图象能否总在直线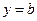 的下方?说明理由;
的下方?说明理由;
(Ⅱ)若函数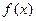 在(0,2)上是增函数,求a的取值范围;
在(0,2)上是增函数,求a的取值范围;
(Ⅲ)设 为方程
为方程 的三个根,且
的三个根,且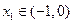 ,
, ,
, ,求证:
,求证: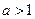 或
或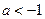
(本小题满分12分)
设函数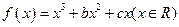 ,已
,已 知
知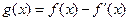
是奇函数.
(Ⅰ)求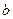 、
、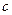 的值;
的值;
(Ⅱ)求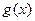 的单调区间与极值.
的单调区间与极值.
(本小题满分12分)
已知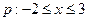 ; q:
; q:
 ,
,
若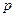 是
是 的充分不必要条件,求实数
的充分不必要条件,求实数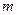 的取值范围。
的取值范围。
(本小题满分12分)
设函数 若
若
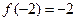 ,
,
求关于 的方程
的方程 的解集.
的解集.
(本小题满分12分)
建造一个容积为16立方米,深为4米的无盖长方体蓄水池,池壁的造价
为每平方米100元,池底的造价为每平方米200元,问怎样设计才能使
该蓄水池的总造价最低,最低造价为多少?