以直角坐标系的原点O为极点, 轴的正半轴为极轴,已知点P的直角坐标为(1,-5),点M的极坐标为(4,
轴的正半轴为极轴,已知点P的直角坐标为(1,-5),点M的极坐标为(4,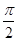 ),若直线
),若直线 过点P,且倾斜角为
过点P,且倾斜角为 ,圆C以M为圆心,4为半径。
,圆C以M为圆心,4为半径。
(I)求直线 的参数方程和圆C的极坐标方程;
的参数方程和圆C的极坐标方程;
(II)试判定直线 与圆C的位置关系。
与圆C的位置关系。
如图AB为圆O直径,P为圆O外一点,过P点作PC⊥AB,
垂是为C,PC交圆O于D点,PA交圆O于E点,BE交PC于F点。
(I)求证:∠PFE=∠PAB;
(II)求证:CD2=CF·CP.
已知函数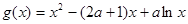
(Ⅰ)当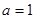 时, 求函数
时, 求函数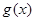 的单调增区间;
的单调增区间;
(Ⅱ)求函数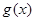 在区间
在区间 上的最小值;
上的最小值;
(Ⅲ) 在(Ⅰ)的条件下,设 ,
,
证明: .参考数据:
.参考数据: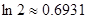 .
.
平面内与两定点 连线的斜率之积等于非零常数
连线的斜率之积等于非零常数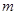 的点的轨迹,加上
的点的轨迹,加上 两点,所成的曲线
两点,所成的曲线 可以是圆,椭圆或双曲线.
可以是圆,椭圆或双曲线.
(Ⅰ)求曲线 的方程,并讨论
的方程,并讨论 的形状与
的形状与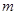 值的关系;
值的关系;
(Ⅱ)当 时,对应的曲线为
时,对应的曲线为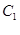 ;对给定的
;对给定的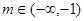 ,对应的曲线为
,对应的曲线为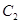 ,若曲线
,若曲线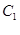 的斜率为
的斜率为 的切线与曲线
的切线与曲线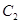 相交于
相交于 两点,且
两点,且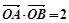 (
( 为坐标原点),求曲线
为坐标原点),求曲线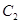 的方程.
的方程.
如图,四棱锥P-ABCD中,底面ABCD是平行四边形,∠ACB=90°,平面PAD⊥平面ABCD,
PA=BC=1,PD=AB=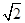 ,E、F分别为线段PD和BC的中点.
,E、F分别为线段PD和BC的中点.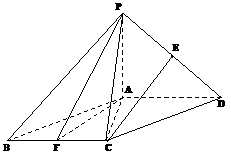
(Ⅰ) 求证:CE∥平面PAF;
(Ⅱ)在线段BC上是否存在一点G,使得平面PAG和平面PGC所成二面角的大小为60°?若存在,试确定G的位置;若不存在,请说明理由.