在天文学中,把两颗相距较近的恒星叫双星,已知两恒星的质量分别为m和M,两星之间的距离为L,两恒星分别围绕共同的圆心作匀速圆周运动,如图所示,求恒星运动的半径和周期。
如图11-2-15所示,在倾角为300的斜面上,放置两条宽L=0.5m的平行导轨,将电源、滑动变阻器用导线连接在导轨上,在导轨上横放一根质量m=0.2kg的金属杆ab,电源电动势E=12V,内阻r=0.3Ω,金属杆与导轨间最大静摩擦力为fm=0.6N,磁场方向垂直轨道所在平面,B=0.8T.金属杆ab的电阻为0.2Ω,导轨电阻不计.欲使杆的轨道上保持静止,滑动变阻器的使用电阻的范围多大?(g取10m/s2) 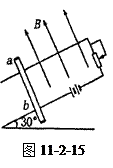
如图11-4-16所示,两块垂直纸面的平行金属板A、B相距d="10.0" cm,B板的中央M处有一个α粒子源,可向各个方向射出速率相同的α粒子,α粒子的比荷q/m=4.82×107 C/kg,为使所有α粒子都不能达到A板,可以在A、B板间加一个电压,所加电压最小值是U0=4.15×104 V;若撤去A、B间的电压,仍使所有α粒子都不能到达A板,可以在A、B间加一个垂直纸面的匀强磁场,该匀强磁场的磁感应强度B必须符合什么条件?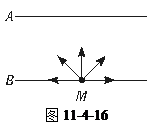
如图11-4-15所示是回旋加速器中的粒子被加速和回旋所在的平面,它的交变电压的频率为1.2×107Hz,半圆形D型盒半径为0.532m,已知氘核的质量m=3.34×10-27kg,电量q=1.6×10-19C.问: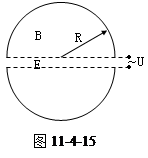
(1)要加速氘核,使之回旋的匀强磁场的磁感应强度应为多大?(答案均保留三位有效数字)
(2)氘核能达到的最大速度是多少?最大动能是多少?
正负电子对撞机的最后部分的简化示意图如图11-3-19所示(俯视图),位于水平面内的粗实线所示的圆环形真空管道是正、负电子作圆周运动的“容器”,经过加速器加速后的正、负电子分别引人该管道时,具有相等的速度v,它们沿管道向相反的方向运动.在管道内控制它们运动的是一系列圆形电磁铁,即图中的n个A1、A2、A3、……An,并且均匀分布在整个圆环上(图中只示意性地用细实线画了几个.其它的用虚线表示),每个电磁铁内的磁场都是匀强磁场,并且磁感应强度都相同,方向都竖直向下.每个磁场区域的直径为d,改变电磁铁内电流的大小,就可改变磁感应强度,从而改变电子偏转角度的大小,经过精确的调整,首先实现了电子沿管道的粗虚线运动,这时电子经每个电磁铁时射入点和射出点都在圆形电磁铁的直径两端,这就为进一步实现正、负电子的对撞作好了准备.
( 1 )试确定正、负电子在管道中分别沿什么方向运动;
(2 )已知正、负电子的质量都是m,所带的电荷为e,重力不计.求电磁铁内磁感应强度的大小.
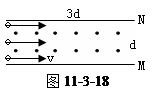
两极板M、N相距为d,板长为3d,两极板都未带电,板间有垂直于纸面向外的匀强磁场,如图11-3-18所示,一群电子沿平行于极板的方向从各个位置以速度V射入板间.为了使电子都不从板间穿出,磁感应强度B的取值范围是怎样的?(设电子电量为e、质量为m)