设 .求
.求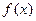 的最大值及最小正周期.
的最大值及最小正周期.
(Ⅰ)设 求
求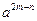 的值;
的值;
(Ⅱ)设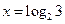 ,求
,求 的值
的值
(本小题满分15分)
已知函数 .
.
(I)求 在
在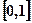 上的最大值;
上的最大值;
(II)若对任意的实数 ,不等式
,不等式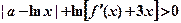 恒成立,求实数
恒成立,求实数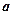 的取值范围;
的取值范围;
(III)若关于 的方程
的方程 在
在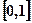 上恰有两个不同的实根,求实数
上恰有两个不同的实根,求实数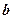 的取值范围.
的取值范围.
(本小题满分15分)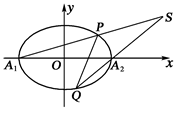
已知椭圆C的离心率e=,长轴的左右端点分别为A1(-2,0),A2(2,0).
(I)求椭圆C的方程;
(II)设直线x=my+1与椭圆C交于P,Q两点,直线A1P与A2Q交于点S,试问:当m变化时,点S是否恒在一条定直线上?若是,请写出这条直线方程,并证明你的结论;若不是,请说明理由.
(本小题满分14分)
在数列{an}中,a1=,并且对于任意n∈N*,且n>1时,都有an·an-1=an-1-an成立,令bn=(n∈N*).
(I)求数列{bn}的通项公式;
(II)求数列{}的前n项和Tn,并证明Tn< -.
(本小题满分14分)
有两辆汽车由南向北驶入四叉路口,各车向左转,向右转或向前行驶的概率相等,且各车的驾驶员相互不认识.
(I)规定:“第一辆车向左转,第二辆车向右转”这一基本事件用“(左,右)”表示。又“(直,左)”表示的是基本事件:“第 一辆车向前直行,第二车向左转”.请参照上面规定列出两辆汽车过路口的所有基本事件;
一辆车向前直行,第二车向左转”.请参照上面规定列出两辆汽车过路口的所有基本事件;
(II)求至少有一辆汽车向左转的概率;
(III)设有 辆汽车向左转,求
辆汽车向左转,求 的分布列和数学期望.
的分布列和数学期望.