(本小题满分15分)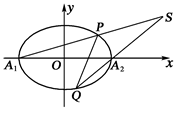
已知椭圆C的离心率e=,长轴的左右端点分别为A1(-2,0),A2(2,0).
(I)求椭圆C的方程;
(II)设直线x=my+1与椭圆C交于P,Q两点,直线A1P与A2Q交于点S,试问:当m变化时,点S是否恒在一条定直线上?若是,请写出这条直线方程,并证明你的结论;若不是,请说明理由.
(本小题满分14分)如图,已知AF 平面ABCD,四边形ABEF为矩形,四边形ABCD为直角梯形,
平面ABCD,四边形ABEF为矩形,四边形ABCD为直角梯形, DAB
DAB ,AB//CD,AD
,AB//CD,AD AF
AF CD
CD 2,AB
2,AB 4.
4. 
(Ⅰ)求证:AC 平面BCE;
平面BCE;
(Ⅱ)求三棱锥A CDE的体积;
CDE的体积;
(Ⅲ)线段EF上是否存在一点M,使得BM CE ?若存在,确定M点的位置;若不存在,请说明理由.
CE ?若存在,确定M点的位置;若不存在,请说明理由.
(本小题满分13分) 已知高二某班学生语文与数学的学业水平测试成绩抽样统计如下表,若抽取学生n人,成绩分为A(优秀)、B(良好)、C(及格)三个等级,设x,y分别表示语文成绩与数学成绩.例如:表中语文成绩为B等级的共有20+18+4=42人.已知x与y均为B等级的概率是0.18.
(Ⅰ)求抽取的学生人数;
(Ⅱ)设该样本中,语文成绩优秀率是30%,求a,b值;
(Ⅲ)已知 ,求语文成绩为A等级的总人数比语文成绩为C等级的总人数少的概率.
,求语文成绩为A等级的总人数比语文成绩为C等级的总人数少的概率.
(本小题满分13分)在△ABC中,角A,B,C的对边分别为a,b,c.已知 ,
, .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)求 的值;
的值;
(Ⅲ)若 ,求△ABC的面积.
,求△ABC的面积.
(本小题满分13分)设数列 的前
的前 项和为
项和为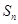 ,点
,点 均在函数
均在函数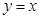 的图象上.
的图象上.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)若 为等比数列,且
为等比数列,且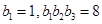 ,求数列
,求数列 的前n项和
的前n项和 .
.
如图,正方体ABCD-A1B1C1D1的棱长为1,点M在棱AB上,且AM ,点P是平面ABCD上的动点,且动点P到直线A1D1的距离与点P到点M的距离的平方差为1,则动点P的轨迹是()
,点P是平面ABCD上的动点,且动点P到直线A1D1的距离与点P到点M的距离的平方差为1,则动点P的轨迹是()
| A.圆 | B.抛物线 | C.双曲线 | D.椭圆 |