（本小题满分14分）如图，已知AF
平面ABCD，四边形ABEF为矩形，四边形ABCD为直角梯形，
DAB
，AB//CD，AD
AFCD2，AB4． 
（Ⅰ）求证：AC
平面BCE；
（Ⅱ）求三棱锥A
CDE的体积；
（Ⅲ）线段EF上是否存在一点M，使得BMCE ?若存在，确定M点的位置；若不存在，请说明理由．
（1）设x、y、z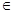
R，且x＋y＋z＝1，求证x2＋y2＋z2≥
；
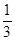（2）设二次函数f (x)＝ax2＋bx＋c（a＞0），方程f (x)－x＝0有两个实根x1，x2，
且满足：0＜x1＜x2＜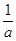
，若x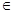(0，x1)。
求证：x＜f (x)＜x1
已知{an}是一个公差大于0的等差数列，且满足a3a6＝55，a2＋a7＝16。
（1）求数列{an}的通项公式；
（2）若数列{an}和数列{bn}满足等式：a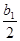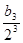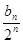n＝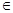
＋
＋
＋……＋
，（n
N+），
求数列{bn}的前n项和Sn。
直线l的方程为（a＋1）x＋y＋2－a＝0（a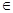
R）。
（1）若l在两坐标轴上的截距相等，求a的值；
（2）若l不经过第二象限，求实数a的取值范围。
如图，四棱锥P—ABCD的底面是正方形，PD⊥底面ABCD，点E在棱PB上。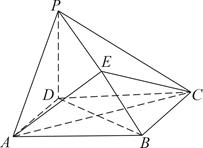
（1）求证：平面AEC⊥PDB；
（2）当PD＝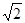
AB且E为PB的中点时，求AE与平面PDB所成角的大小。
已知△ABC中，A（1，1），B（m，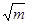
），C（4，2），1＜m＜4。
求m为何值时，△ABC的面积S最大。