(1)设x、y、z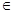 R,且x+y+z=1,求证x2+y2+z2≥
R,且x+y+z=1,求证x2+y2+z2≥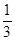 ;
;
(2)设二次函数f (x)=ax2+bx+c(a>0),方程f (x)-x=0有两个实根x1,x2,
且满足:0<x1<x2<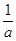 ,若x
,若x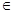 (0,x1)。
(0,x1)。
求证:x<f (x)<x1
设函数 ,其中
,其中 为正整数.
为正整数.
(1)判断函数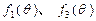 的单调性,并就
的单调性,并就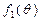 的情形证明你的结论;
的情形证明你的结论;
(2)证明: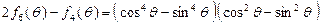 ;
;
(3)对于任意给定的正整数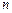 ,求函数
,求函数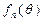 的最大值和最小值.
的最大值和最小值.
(本小题满分12分)
已知点 ,点
,点 在
在 轴上,点
轴上,点 在
在 轴的正半轴上,点
轴的正半轴上,点 在直线
在直线 上,且
上,且
满足 .
.
(Ⅰ)当点 在
在 轴上移动时,求点
轴上移动时,求点 的轨迹
的轨迹 的方程;
的方程;
(Ⅱ)设 、
、 为轨迹
为轨迹 上两点,且
上两点,且 >1,
>1,  >0,
>0, ,求实数
,求实数 ,
,
使 ,且
,且 .
.
(本小题满分12分) 已知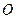 为坐标原点,点
为坐标原点,点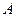 、
、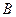 分别在
分别在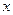 轴、
轴、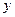 轴上运动,且
轴上运动,且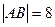 ,动点
,动点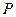 满足
满足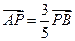 ,设点
,设点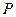 的轨迹为曲线
的轨迹为曲线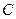 ,定点
,定点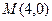 ,直线
,直线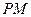 交曲线
交曲线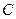 于另外一点
于另外一点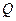 .
.
(1)求曲线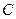 的方程;
的方程;
(2)求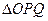 面积的最大值.
面积的最大值.
(本小题满分13分)如图,已知椭圆的中心在原点,焦点在x轴上,长轴长是短轴长的2倍且经过点M(2,1),平行于OM的直线L在y轴上的截距为m(m≠0),L交椭圆于A、B两个不同点。
(1)求椭圆的方程;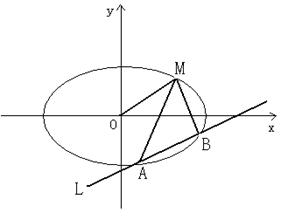
(2)求m的取值范围;
(3)求证直线MA、MB与x轴始终围成一个等腰三角形。
已知数列( )与{
)与{ )有如下关系:
)有如下关系: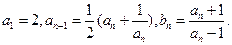
(1)求数列( }的通项公式。
}的通项公式。
(2)设 是数列{
是数列{ }的前n项和,当n≥2时,求证
}的前n项和,当n≥2时,求证 :
: