已知{an}是一个公差大于0的等差数列,且满足a3a6=55,a2+a7=16。
(1)求数列{an}的通项公式;
(2)若数列{an}和数列{bn}满足等式:an=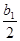 +
+ +
+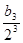 +……+
+……+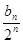 ,(n
,(n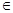 N+),
N+),
求数列{bn}的前n项和Sn。
((本题12分)已知P与平面上两定点A ,B
,B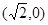 连线的斜率的积为定值
连线的斜率的积为定值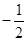 ,
,
(Ⅰ)试求动点P的轨迹方程C;
(Ⅱ)设直线 与曲线C交于M、N两点,当|MN|=
与曲线C交于M、N两点,当|MN|= 时,求直线
时,求直线 的方程。
的方程。
((本题12分)如图2,在棱长为1的正方体ABCD—A1B1C1D1中,点E、F、G分别是DD1、BD、BB1的中点。
(Ⅰ)求直线EF与直线CG所成角的余弦值;
(Ⅱ)求直线C1C与平面GFC所成角的正弦值;
(Ⅲ)求二面角E—FC—B的余弦值。
(本题12分)求过两圆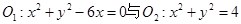 的交点,
的交点,
(Ⅰ)且过M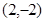 的圆
的圆 的方程;
的方程;
(Ⅱ)且圆心在直线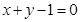 上的圆
上的圆 的方程。
的方程。
(本题12分)已知△ABC的三个顶点坐标分别为A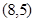 , B
, B ,C
,C ,
,
(Ⅰ)求AC边上的中线所在直线方程;
(Ⅱ)求AB边上的高所在直线方程;
(Ⅲ)求BC边的垂直平分线的方程。
、如图,椭圆E经过点 ,对称轴为坐标轴,焦点F1,F2在
,对称轴为坐标轴,焦点F1,F2在 轴上,离心率
轴上,离心率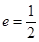 ,
,
⑴求椭圆E的方程;
⑵求∠F1AF2的角平分线所在的直线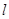 的方程;
的方程;
⑶在椭圆E上是否存在关于直线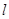 对称的相异两点?若存在,请找出;若不存在,说明理由。
对称的相异两点?若存在,请找出;若不存在,说明理由。