(本小题14分)在等比数列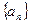 中,
中,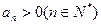 ,公比
,公比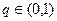 ,且
,且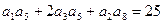 ,又
,又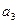 与
与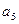 的等比中项是2,
的等比中项是2,
(1)求数列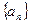 的通项公式;
的通项公式;
(2)设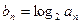 ,数列
,数列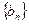 的前
的前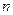 项和为
项和为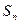 ,求
,求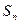 .
.
(本小题12分)已知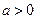 且
且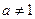 ,命题P:函数
,命题P:函数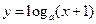 在区间
在区间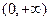 上为
上为
减函数;命题Q:曲线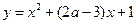 与
与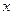 轴相交于不同的两点.若
轴相交于不同的两点.若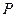 为真,
为真,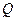 为假,
为假,
求实数 的取值范围.
的取值范围.
(本小题12分)在△ABC中,已知B=45°,D是BC边上的一点,AD=10,AC=14,DC=6,求AB的长.
本题14分)已知动圆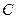 过点
过点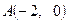 ,且与圆
,且与圆 相内切.
相内切.
(1)求动圆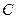 的圆心
的圆心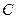 的轨迹方程;
的轨迹方程;
(2)设直线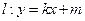 (其中
(其中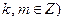 与(1)中所求轨迹交于不同两点
与(1)中所求轨迹交于不同两点 ,
, ,与双曲线
,与双曲线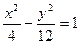 交于不同两点
交于不同两点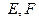 ,问是否存在直线
,问是否存在直线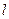 ,使得向量
,使得向量 ,若存在,指出这样的直线有多少条?若不存在,请说明理由.
,若存在,指出这样的直线有多少条?若不存在,请说明理由.
(本题14分)已知点(1, )是函数
)是函数 且
且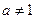 )的图象上一点,等比数列
)的图象上一点,等比数列 的前
的前 项和为
项和为 ,数列
,数列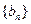
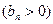 的首项为
的首项为 ,且前
,且前 项和
项和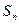 满足
满足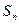 -
- =
= +
+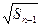 (
( ).
).
(1)求数列 和
和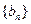 的通项公式;
的通项公式;
(2)若数列{ 前
前 项和为
项和为 ,问
,问 的最小正整数
的最小正整数 是多少? .
是多少? .