(本题14分)已知点(1, )是函数
)是函数 且
且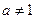 )的图象上一点,等比数列
)的图象上一点,等比数列 的前
的前 项和为
项和为 ,数列
,数列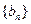
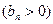 的首项为
的首项为 ,且前
,且前 项和
项和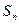 满足
满足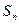 -
- =
= +
+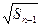 (
( ).
).
(1)求数列 和
和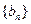 的通项公式;
的通项公式;
(2)若数列{ 前
前 项和为
项和为 ,问
,问 的最小正整数
的最小正整数 是多少? .
是多少? . 
(本小题满分12分)
已知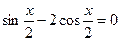 .
.
(1)求 的值;
的值;
(2)求 的值.
的值.
(本小题满分14分)
已知函数 (
(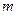 ,
,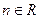 ,
, 且
且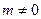 )的图象在
)的图象在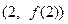 处的切线与
处的切线与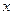 轴平行.
轴平行.
(I) 试确定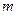 、
、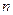 的符号;
的符号;
(II) 若函数 在区间
在区间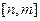 上有最大值为
上有最大值为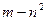 ,试求
,试求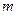 的值.
的值.
(本小题满分14分)
在数列 中,
中,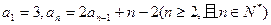
(1)求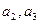 的值;
的值;
(2)证明:数列 是等比数列,并求
是等比数列,并求 的通项公式;
的通项公式;
(3)求数列 。
。
(本小题满分14分)
已知圆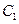 :
: 和圆
和圆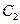 ,直线
,直线
 与圆
与圆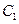 相切于点
相切于点 ;圆
;圆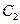 的圆心在射线
的圆心在射线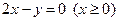 上,圆
上,圆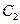 过原点,且被直线
过原点,且被直线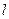 截得的弦长为
截得的弦长为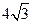 .
.
(Ⅰ)求直线 的方程;
的方程;
(Ⅱ)求圆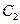 的方程.
的方程.
(本小题满分14分 )
)
如图,已知正三棱柱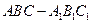 的底面边长是
的底面边长是 ,
, 、E是
、E是 、BC的中点,AE=DE
、BC的中点,AE=DE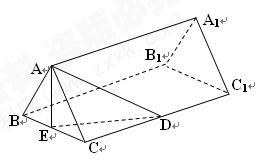
(1)求此正三棱柱的侧棱长;
(2)求正三棱柱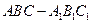 表面积.
表面积.