如图所示,竖直平面内有一半径为、电阻为、粗细均匀的光滑半圆形金属环,在、处与相距为、电阻不计的平行光滑金属轨道、相接,之间接有电阻,已知=12,=4。 在MN上方及下方有水平方向的匀强磁场和,磁感应强度大小均为。现有质量为、电阻不计的导体棒,从半圆环的最高点处由静止下落,在下落 过程中导体棒始终保持水平,与半圆形金属环及轨道接触良好,设平行轨道足够长。已知导体棒下落/2时的速度大小为,下落到处的速度大小为。
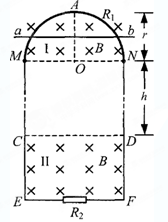
(1)求导体棒从下落/2时的加速度大小。
(2)若导体棒进入磁场Ⅱ后棒中电流大小始终不变,求磁场I和Ⅱ之间的距离和上的电功率。
(3)若将磁场Ⅱ的边界略微下移,导体棒刚进入磁场Ⅱ时速度大小为,要使其在外力作用下做匀加速直线运动,加速度大小为,求所加外力随时间变化的关系式。
如图所示,滑块以某一速率靠惯性沿固定斜面由底端A向上运动,到达最高点B时离地面的高度为H,然后又沿斜面返回,到出发点A时的速率为原来速率的一半。若取斜面底端重力势能为零,求上升过程中滑块动能等于势能的位置离地面的高度h。
在一次抗洪抢险活动中,解放军某部运用直升机抢救一重要落水物体,在静止在空中的直升机上用电动机通过悬绳将物体从离飞机90m处的洪水中吊到机舱里,已知物体的质量为80kg,吊绳的拉力不能超过1200N,电动机的额定输出功率为12kW,为尽快把物体安全救起,操作人员采取的办法是:先让吊绳以最大的拉力工作一段时间,达额定功率后电动机以额定功率工作,当物体到达机舱时它达到最大速度。(g=10m/s2)
求:(1)落水物体刚到达机舱时的速度;
(2)这一过程所用的时间。
某司机在平直公路上测试汽车的制动性能。他从车上速度表看到汽车速度的大小为v=72km/h时紧急刹车,由于车轮与公路面的摩擦,车轮在公路面上划出一道长L=40m的刹车痕迹后停止。求:
(1)车轮与公路面间的动摩擦因数μ;
(2)该司机驾车仍以v=72km/h的速度在一段动摩擦因数也为μ、倾角为8°的坡路上匀速
向下行驶,发现前方停着一辆故障车。若刹车过程司机的反应时间为△t=0.7s,为了避免两
车相撞,该司机至少应在距故障车多远处采取同样的紧急刹车措施?
(取sin8°="0.14," cos8°=0.99,g=10m/s2)
如图,水平长传送带始终以3m/s的速度匀速运动。现将一质量为1kg的物块轻放于左端,最终物块和传送带一起以3m/s的速度运动,在物块由速度为零增加至3m/s的过程中,求:
(1)物块和传送带间由于摩擦而产生的热量。
(2)由于放了物块,带动传送带的电动机多消耗多少电能?
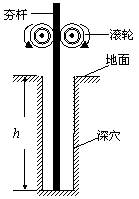
如图所示是建筑工地上常用的一种“深穴打夯机”。工作时,电动机带动两个紧压夯杆的滚轮匀速转动将夯杆从深为h的坑中提上来,当两个滚轮彼此分开时,夯杆被释放,最后夯杆在自身重力的作用下落回深坑,夯实坑底;然后两个滚轮再次压紧,夯杆再次被提上来,如此周而复始工作。已知两个滚轮边缘的线速度v恒为4m/s,每个滚轮对夯杆的正压力FN =2×104 N,滚轮和夯杆间的动摩擦因数μ =" 0.3" ,夯杆的质量m =1×10 3kg,坑深h ="6.4m" 。假定在打夯的过程中坑的深度变化不大,且夯的低端升到坑口时,速度正好为零。取g =10m/s2。试求:
(1)夯杆上升的过程中,被滚轮释放时它的速度为多大?
此时夯杆低端离坑底多高?
(2)每个打夯周期中,电动机对夯杆所做的功为多少?
(3)每个打夯周期中,由于摩擦产生的热量。
(4)打夯周期T.