在长为100千米的铁路线AB旁的C处有一个工厂，工厂与铁路的距离CA为20千米.由铁路上的B处向工厂提供原料，公路与铁路每吨千米的货物运价比为5∶3，为节约运费，在铁路的D处修一货物转运站，设AD距离为x千米，沿CD直线修一条公路(如图).
(1)将每吨货物运费y(元)表示成x的函数.
(2)当x为何值时运费最省？
（共12分）已知函数
直线
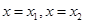是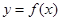
图像的任意两条对称轴，且
的最小值为
．
（1）求函数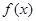
的单调增区间；
（2）求使不等式
的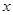
的取值范围．
（3）若
求
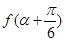的值；
（共10分）
（1）解不等式：
；
（2）解关于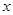
的不等式：
（本小题满分13分）如图，在平面直角坐标系
中，点
在单位圆
上，
，且
．
（1）若
，求
的值；
（2）若
也是单位圆上的点，且
．过点
分别做
轴的垂线，垂足为
，记
的面积为
，
的面积为
．设
，求函数
的最大值．
（本小题13分）已知函数
的一系列对应值如下表：
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|
|
（1）根据表格提供的数据求函数
的解析式；
（2）求函数的单调递增区间和对称中心；
（3）若当
时，方程
恰有两个不同的解，求实数
的取值范围．
（本小题满分12分）（如图，某海滨浴场的岸边可近似地看成直线，位于岸边A处的救生员发现海中B处有人求救，救生员没有直接从A处游向B处，而是沿岸边自A跑到距离B最近的D处，然后游向B处，若救生员在岸边的行进速度为6米/秒，在海中的行进速度为2米/秒，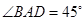
。
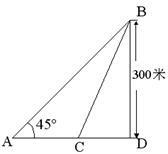
（1）分析救生员的选择是否正确；
（2）在AD上找一点C，使救生员从A到B的时间为最短，并求出最短时间。